Il teorema di Fermat relativo alle funzioni.

Il Teorema di Fermat relativo alle funzioni di una variabile reale è un Teorema fondamentale che lega il calcolo differenziale al problema della ricerca di estremi locali di una funzione reale di variabile reale. L’idea (che risale allo stesso Fermat) è che una funzione attorno ad un suo estremo è stazionaria: ovvero una funzione attorno ad un suo estremo si comporta quasi come se fosse costante.

Teorema di Fermat: Sia data una funzione derivabile f : (a,b) → R. Supponiamo che c ∈(a,b) sia un punto di minimo (o massimo) locale per f; allora f'(c)=0.

Dimostrazione. Consideriamo

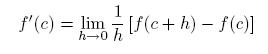
Supponiamo che c sia punto di minimo locale (se c fosse punto di massimo locale la dimostrazione sarebbe la stessa, a meno di ovvie modifiche). Essendo c punto di minimo locale, per h>0 abbastanza piccolo si ha che f(c+h)≥f(c); ne segue che f'(c)≥0, essendo limite di una funzione non-negativa. Per h<0 abbastanza piccolo si ha ancora f(c+h)≥f(c), ma stavolta il rapporto incrementale risulta negativo, avendosi numeratore positivo e denominatore negativo; ne segue che f'(c)≤0. Ma allora deve essere f'(c)=0, che conclude la dimostrazione.

Tale Teorema si applica alla ricerca dei punti di minimo o massimo locali per funzioni derivabili; infatti a norma del precedente Teorema gli unici possibili punti candidati ad essere di massimo o minimo locale per f (punti interni all’intervallo) sono i cosidetti punti critici, ovvero i punti x per cui f'(x)=0. Non è detto però che tali punti siano necessariamente o punti di minimo o punti di massimo locale; è ben noto che una funzione potrebbe avere un punto critico detto di flesso a tangente orizzontale, che non è quindi nè di minimo nè di massimo locale. Esempio: la funzione f(x)=x³ ha in x=0 un punto di flesso a tangente orizzontale, essendo f'(0)=0, ma non essendo x=0 nè di minimo nè di massimo locale per f.