I numeri complessi trovano applicazione in tutti i campi in cui si
debbano trattare segnali periodici.
Il caso più semplice è quello del calcolo dei circuiti
in corrente alternata.
Si dimostra infatti che la classica legge di Ohm e le altre leggi
dei circuiti, valide per
quantità (correnti, tensioni) costanti, valgono anche per
quantità periodiche, purché
i valori degli elementi passivi (elementi resistivi, induttivi
e capacitivi) siano rappresentati mediante numeri complessi (impedenze).
Le quantità (tensioni e correnti) risultanti dai calcoli
sono in genere numeri complessi il cui modulo rappresenta il valore
di picco della sinusoide e la fase il ritardo (o anticipo) del segnale
di uscita rispetto a quello di ingresso.
In appendice gli interessati possono trovare un esempio
pratico di calcolo di un circuito in regime sinusoidale.
Altre usi
nel campo dell’elettronica
non tanto dei semplici numeri complessi, quanto
dell’algebra complessa in generale,
riguardano anch’esse
i segnali periodici e si possono ricondurre alla cosiddetta
analisi di Fourier che ha numerosissime applicazioni
nel campo delle trasmissioni,
dell’amplificazione e registrazione sonora,
dell’ elaborazione dei segnali,
per citarne solo alcune fra le più diffuse.
Appendice: Esempio pratico
Nota: per proseguire occorrono un po’ di nozioni di calcolo elementare con
i numeri di complessi e di teoria dei circuiti elettrici!
Senza entrare in dettagli, per cui rimando a qualche testo di
elettrotecnica elementare, vediamo un caso semplice mostrato nello
schema seguente (figura A):
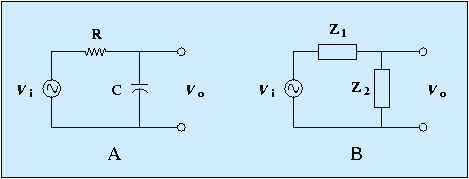
Nella figura B è rappresentato lo stesso circuito evidenziando le
generiche impedenze degli elementi passivi.
Supponiamo di voler calcolare il segnale Vo (tensione in uscita)
dati il segnale di ingresso Vi ed i
parametri del circuito (supponiamo R=1000 Ohm e C=0.001 Farad).
Il segnale di ingresso è rappresentato da un numero complesso
con parte immaginaria zero (ciò corrisponde a considerare come
fase di riferimento quella del segnale di ingresso),
diciamo Vi=(5, 0) corrispondente alla tensione di 5 volt.
L’impedenza dell’elemento resistivo è
anch’essa rappresentata da un numero con parte
immaginaria nulla (i resistori ideali non introducono sfasamento):
Z1=(1000, 0).
L’impedenza dell’elemento capacitivo
è rappresentata da un numero con parte reale nulla
e parte immaginaria negativa (la capacità ideale introduce uno
sfasamento di -90o) e pari al reciproco della capacità:
Z2=(0, -1000).
Applicando le regole per il calcolo del circuito:
Vo = Vi * Z2 / (Z1 + Z2)
Cioè in pratica:
Vo = (5, 0) * (0, -1000) / ((1000, 0)+(0, -1000)) =
(2.5, -2.5)
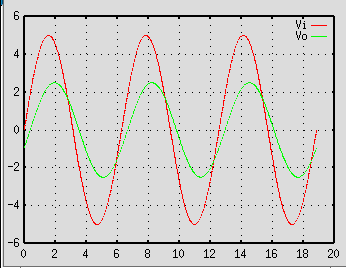
Ovvero il segnale di uscita risulta una sinusoide con valore di picco
pari a 2.5 volt (modulo del numero complesso) e con un ritardo di fase di 45o rispetto al
segnale di ingresso: