I filtri sono oggetti comunemente usati negli apparati radioelettronici e ottici.
In tutti i sistemi dove si vuole che il transito di segnali non voluti subisca la massima attenuazione possibile (banda d’arresto) ed i segnali voluti abbiano una minore attenuazione possibile (banda passante) occorre utilizzare i filtri.
In base alla posizione, sull’asse delle frequenze, della banda d’arresto rispetto alla banda passante otteniamo filtri di tipo: passa-basso, passa-alto, passa-banda e stoppa-banda
La risposta del filtro ampiezza-frequenza e fase–frequenza può soddisfare una ben precisa funzione di trasferimento matematica (Butterworth,Tschebyscheff, Bessel, gaussiani, coseno rialzato, ellittici ecc ) oppure è possibile approssimare la forma richiesta mediante una funzione polinomiale razionale fratta.
Oltre all’utilizzo descritto, vi sono altre due fondamentali esigenze di filtraggio nei sistemi di telecomunicazioni: la sagomatura del canale ed il filtro di rumore,
- La risposta ampiezza frequenza del ricevitore deve essere adattata alla forma dello spettro del segnale. In particolare per le trasmissioni digitali è fondamentale, pena il peggioramento della sensibilità del ricevitore, che la risposta all’impulso del canale complessivo deve essere sagomata secondo i criteri di Nyquist. La trasformata in frequenza di detta risposta impulsiva, richiede l’uso di filtri con particolari sagomature d’ampiezza e fase assolutamente lineare, la più usata è quella a coseno rialzato.
- Prima di decidere il contenuto del digitale trasmesso (audio, video e dati) o di vedere ( occhi) o sentire (orecchie) nel caso di trasmissioni analogiche, occorre massimizzare il rapporto segnale –rumore tramite un filtro. Il filtro di rumore deve essere molto stretto per ridurre il più possibile la potenza di rumore (KTB) ma non molto stretto da deformare il segnale.
I filtri possono essere realizzati in una vasta gamma di componentistica. Dai classici filtri ad induttanza e capacità a costante concentrate o distribuite ai filtri piezoelettrici e meccanici. Dai filtri attivi a resistenza e capacità agli switch capacitor. Dai filtri a linea di ritardo ai filtri numerici.
I Filtri FIR, a risposta dell’impulso finita ed i filtri IIR a risposta dell’impulso infinita, sono ottenuti pesando e sommando opportunamente gli echi, ritardati da celle di ritardo, del segnale d’ingresso.
Essi iniziano a trovare impiego, prendendo il nome di filtri digitali, come unica soluzione senza valide alternative per la sagomatura del canale, a metà anni settanta sui sistemi di modemodulazione digitali (in particolar modo i FIR).
Da un decennio con la tecnologia DSP, Digital Signal Processing, i filtri digitali si sono imposti come soluzione ideale a problematiche applicative di media ed elevata complessità nella maggior parte dei campi tecnici. L’analisi e la sintesi dei segnali vocali, l’elaborazione delle immagini, l’audio digitale, l’automazione, la strumentazione biomedicale e di laboratorio, e in generale l’elettronica destinata alle applicazioni consumer, sono solo alcune delle applicazioni dei filtri digitali.
Filtri FIR
I filtri FIR, Finite Impulse Response, sono del tipo ad anello aperto. Le loro uscite sono esclusivamente in funzione di un numero finito di segnali d’ingresso e non hanno alcun elemento di reazione. Rispetto ai filtri IIR presentano i seguenti vantaggi:
- La funzione di trasferimento dei filtri FIR non ha poli, ma solo zeri; di conseguenza la loro uscita è sempre finita è stabile. Sotto questo punti di vista i FIR non hanno un esatto equivalente analogico come i filtri IIR.
- I filtri FIR hanno una risposta lineare in fase ( il ritardo di fase aumenta linearmente con la frequenza del segnale d’ingresso) indispensabile al trattamento di segnali digitali e analogici televisivi
- Bassa sensibilità alla precisione dei coefficienti c. I filtri FIR sono più facili da capire che progettare.
- Facilità di sviluppo di filtri adattativi (equalizzano il canale in tempo reale per adeguarsi a condizioni esterne variabili,fading selettivi).
L’architettura classica dei filtri FIR, valida come analisi, per tutte le realizzazioni1 (analogiche, digitali e numeriche ) è la seguente:

E’ interessante osservare come questo schema può anche essere il modello di un segnale riflesso che si somma con il segnale diretto tra il percorso di un’antenna trasmittente e l’antenna ricevente.
Il fading selettivo, (multipath) non è altro che l’effetto di un filtro FIR, non voluto tra il trasmettitore e ricevitore.
Il modulo della funzione di trasferimento del FIR ad un solo tap, (vedi Nota 2) è uguale a:
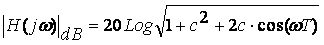
Come esempio, fissiamo un ritardo T= 100ns (che corrisponde ad una differenza di percorso trai raggi (diretto e riflesso) di circa 30 metri3 ed un valore di c di 0,9 e 0,7 otteniamo tra i 150 e 170 Mhz la seguente risposta ampiezza frequenza:
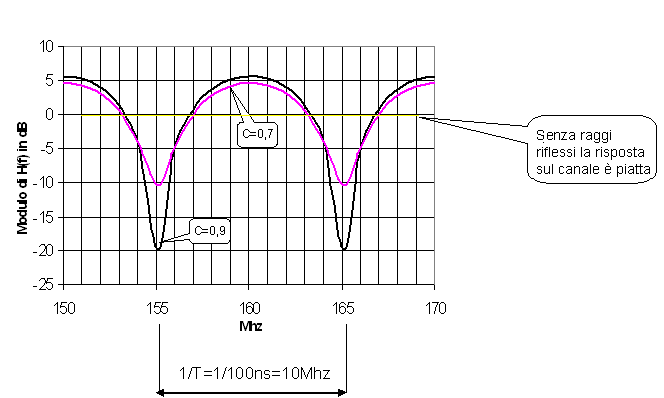
I notches sono periodici e si ripetono in frequenza ogni 1/T.
Ovviamente per approssimare una funzione di trasferimento H(f) voluta,servono più taps e opportuni valori dei coefficienti c .
Con i filtri FIR non si riesce a realizzare la classica funzione con poli e zeri. Si ricava la risposta all’impulso h(t) dalla risposta in frequenza H(f) che si vuole ottenere (antitrasformata).
Si può dimostrare che i valori dei coefficienti rappresentano l’istogramma dei valori discreti di distanza T della risposta all’impulso h(t) che si vuole realizzare.
Se l’impulso è simmetrico ( fase lineare ) la funzione è pari è i coefficienti saranno di valore simmetrico attorno al massimo valore centrale.
Più fitti sono i campioni, T << del tempo di bit del segnale x(t), maggiore sarà il numero di taps da realizzare e migliore sarà l’approssimazione del filtro.
In cascata al filtro FIR è richiesto un filtro detto antialiasing per eliminare la periodicità a distanza 1/T. Nei DSP dove tutto è all’interno di un chip si usano come antialasing strutture di filtri IIR.
Filtri IIR
La classica struttura dei filtri IIR, Infinite Impulse Response, è rappresentata in figura.
Il filtro IIR può essere visto come una cascata di due blocchi. Un blocco è la classica struttura di un filtro FIR con N ritardi e il secondo blocco dove il segnale d’uscita y(t) è prelevato, ritardato, pesato e riportato all’ingresso (reazione).
L’uscita y(t) è definita non solo dal risultato del filtro FIR v(t) ma anche dai valori d’uscita reazionati nel circuito.
La retroazione è negativa, altrimenti una reazione positiva con guadagno maggiore di uno trasformerebbe il filtro in un oscillatore. Sono filtri molto critici ad ottenere la stabilità voluta.
Il ritardo di fase, dei filtri, non è lineare con la frequenza, quindi non sono adatti per la sagomatura di canale. L’unico vantaggio rispetto ai filtri FIR, data la presenza di poli, é che richiedono minori tap ( anche un terzo)a parità d’ordine di filtro da realizzare.

La funzione di trasferimento presenta sia zeri che poli.
Il numero di zeri è N (come i FIR) il numero di poli è determinato dal numero di M.
Tutti i filtri IIR hanno un equivalente filtro analogico. (Il classico integratore R-C, filtro passa-basso, si realizza con un IIR ,ed una sola cella di ritardo M=1 e N=0).
Questa caratteristica è sfruttata come uno dei metodi per il calcolo dei coefficienti.
Si progetta il filtro come se si dovesse realizzare un classico filtro analogico.
Si rappresenta la funzione in poli e zeri nel dominio di s (trasformata di Laplace) mappandoli nel classico piano complesso e si converte nel dominio di z ( trasformata per segnali discreti).
L’H(z) ottenuta contiene il valore dei coefficienti c per gli zeri e valori di b per i poli.
Come per tutti i filtri,la sintesi,l’analisi e la complessità aumentano con l’aumentare del grado della funzione che si deve realizzare.
Avrei tante cose da aggiungere ma ritengo di aver detto fin troppo vista la generalità della domanda.
Avendo progettato decine e decine di filtri digitali ho cercato di divulgare gli aspetti meno noti in modo che chi volesse approfondire si renda conto di cosa cercare.
Note
1) Per una trattazione generale rappresento x(t) come funzione continua del tempo.
Per i segnali discreti, x(t) è da intendersi come x(nT) dove n è il numero di campioni nel tempo di campionamento T.
Si ricorda che tutti i segnali digitali a tempo discreto trasmessi su un mezzo trasmissivo ( cablato o wireless ) in ricezione diventano segnali a tempo continuo come se fossero d’origine analogica.
Per sagomare il canale si usavano filtri FIR, dove i ritardi erano realizzati con rocchetti di cavetto coassiale o linee di ritardo ad induttanza e capacità ed i valori dei coefficienti c e la loro somma erano ottenuti mediante partitori resistivi.
I coefficienti negativi si ottenevano interponendo un amplificatore invertente tra l’uscita del Tap ed il nodo somma.
Il decisore dei bit trasmessi era uno squadratore e si otteneva un segnale rappresentato da due soli bit e trattato dalle classiche porte (Flip-flop, OR, NOR, ecc ).
Il massimo risultato della moltiplicazione,fatta con Ex-OR, era il risultato di segno tra i fattori.
Quando la componentistica permise di usare tecniche DSP (tramite ASIC) convertendo il segnale continuo nel tempo in un numero, s’iniziò a fare diversi calcoli sui segnali.
In questo caso il segnale x(nT) è da intendersi come un segnale quantizzato, codificato a m bit. (In sostanza un bus di m fili paralleli)
I ritardi T sono delle memorie tipo RAM e prima di sommare i segnali ritardati, l’uscita dei Tap a m bit è fatta moltiplicare con il valore dei coefficienti inseriti in una ROM. Normalmente rappresentato da numeri di 12 a 16 bit per i FIR e 16-24 bit per gli IIR.
Per differenziare la diversità del trattamento del segnale rispetto alle classiche operazioni digitali si cercò di divulgare questi sistemi come numerici rispetto ai precedenti sistemi digitali.
Oggi nel linguaggio comune si alterna la parola numerica e digitale per dire la stessa cosa.
Conviene quindi adottare, come gli americani,il termine DSP quando sui segnali ,trattati come numeri,vengono fatti dei calcoli (In fondo i FIR ed gli IIR sono somme di prodotti di segnali ritardati).
2) Tenendo come riferimento lo schema ad un solo tap, calcoliamo la risposta ampiezza-frequenza:

3) L’onda elettromagnetica nello spazio libero percorre un metro in circa 3,3 nS come la luce.
La differenza di lunghezza del percorso tra raggio riflesso e diretto è uguale 100nS/3,3 nS/m =30m
Bibliografia
- La bibbia dei FIR e IIR è: J.Proakis, D.Manolakis “Digital Signal Processing” Prentice Hall. Terza edizione
- Un buon SW di progettazione e simulazione di FIR e IIR è Matlab.