L’espresione da lei
cercata, la somma dei primi n
quadrati perfetti è
![]() [1]
[1]
Rammentiamo brevemente
che la somma dei primi n numeri
naturali è
![]()
[2]
La leggenda vuole
che a scoprirla sia stato il genio di Gauss, in tenera età, grazie ad
una elegante intuizione geometrica. Si osservi la figura 1:
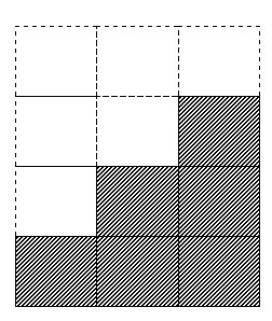
Fig. 1: La somma dei primi n naturali è pari alla semiarea del rettangolo di lati n ed n+1
La chiave risolutiva
è l’osservazione che il numero di quadrati tratteggiati (ovvero la somma
dei primi 3 numeri naturali) è pari alla semiarea del triangolo di lati
4 e 3. Da qui, la [2].
La formale dimostrazione
della 1, ottenuta intuitivamente, si completa utilizzando il principio di induzione:
Sia p(n) una proprietà,
1)
se p(n) è verificata per n=0 (passo base del principio di induzione)
2)
se p(n) è verificata implica (ipotesi induttiva)
che p(n+1) è verificata
allora p(n) è verificata per tutti i numeri naturali
n.
Al lettore va l’esercizio
di applicazione del principio d’induzione alla dimostrazione della [2].
Confesso che il quesito
del lettore mi ha dato da pensare un bel pò. Alla fine, la chiave per
ricavare l’espressione cercata sta proprio nell’uso di un criterio geometrico.
Si osservi la fig.
2:
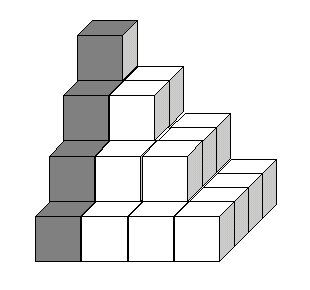
Fig. 2: Solido con volume pari alla somma dei primi
n quadrati perfetti
La figura 2 è ottenuta impilando i quadrati di lato 1×1, 2×2, 3×3 e 4×4.
La somma dei primi n quadrati perfetti è quindi pari al numero
di cubetti della figura costruita reiterando n volte il procedimento.
Ora, si prenda un
coltello ben affilato e si affetti la figura 2 partendo dai cubetti grigi
di sinistra e si osservi la figura ritagliata. A cosa assomiglia ?
Il numero di cubetti
ritagliati è pari alla somma dei primi 4 numeri naturali !
A questo punto, reiterariamo
il processo e consideriamo la differenza in numero di cubetti tra
il taglio corrente ed il primo taglio:
Primo taglio: 10 cubetti
eliminati
Secondo taglio: 9 cubetti eliminati,
differenza : 10-9 = 1
Terzo taglio: 7 cubetti eliminati,
differenza: 10-7 = 3
Quarto taglio: 4 cubetti eliminati,
differenza: 10-4=6
quanto vale la differenza,
nei passi successivi ?
La differenza è pari, di nuovo,
alla somma dei primi n numeri naturali !
Si immagini ora di costruire
la figura 2 utilizzando un numero n
qualsiasi di cubetti.
·
Al primo taglio si elimineranno
n(n+1)/2 cubetti.
·
Al secondo taglio si
elimineranno n(n+1)/2 cubetti
meno la differenza: la somma del primo numero naturale, cioè 1
·
Al terzo taglio si elimineranno
n(n+1)/2 cubetti meno la differenza:
la somma dei primi 2 numeri naturali, cioè 3
·
Al quarto taglio si elimineranno
n(n+1)/2 cubetti meno la differenza:
la somma dei primi 3 numeri naturali, cioè 6
·
All’i-mo taglio si elimineranno
n(n+1)/2 cubetti meno la differenza:
la somma dei primi i-1 numeri naturali, cioè i(i+1)/2
Possiamo contare il
numero di cubetti che compongono la figura 2 affettandola in n passi.
Più formalmente:
![]() [3]
[3]
e valutiamone i termini
singolarmente.
![]() [4]
[4]
perché sommatoria
in n-1 passi di termini indipendenti dalla
variabile iterativa i.
![]() [5]
[5]
perché la sommatoria
gode della proprietà distributiva ![]() .
.
Introduciamo inoltre
il seguente artifizio sugli indici della sommatoria:
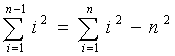 [6]
[6]
che ci consente di
rendere confrontabile il termine sommatoria di i2 della [5] con il primo membro della [3] (attenzione:
l’estremo superiore della sommatoria è stato portato da n-1 ad n).
Per cui, la [5] diviene:
![]() [7]
[7]
A questo punto si
sostituiscono le espressioni [4] e [7] nella [3] (occhio ai segni !):
![]()
facciamo il minimo
comune multiplo:
![]()
la sommatoria al secondo
membro non deve preoccuparci: basta portarla al primo !
![]()
ancora un piccolo
minimo comune multiplo:
![]()
Da qui, abbiamo quasi
vinto – matto in due mosse – si semplificano i termini:
![]()
e si fattorizza,
![]()
scacco matto !