Malgrado abbia l’aspetto
di un indovinello, questa domanda non è priva di
interesse.
Per chiarezza,
preferisco rispondere alla seguente domanda
“preliminare”: “in un orologio a
lancette ideale, ogni quanto tempo
la lancetta delle ore e quella dei minuti si
sovrappongono esattamente?“.
Per rispondere vi sono
due approcci, uno analitico ed uno sintetico.
Per iniziare con
l’approccio analitico, consideriamo un orologio ideale,
che in questo contesto definiamo come un orologio con
lancette delle ore e dei minuti infinitamente sottili
(della lancetta dei secondi ci disinteressiamo
completamente) che si muovono di moto circolare uniforme
(cioè con moto continuo, e non a scatti come di solito
invece avviene). L’orologio ideale ha una meccanica
perfetta, cosicché tra le velocità angolari delle due
lancette vi è esattamente un rapporto 1 a 12. Per
comodità, misureremo gli angoli in gradi sessagesimali e
il tempo in minuti.
Se indichiamo con vm
la velocità angolare della lancetta dei minuti e con vh
quella della lancetta delle ore, le leggi di moto
angolare delle due lancette sono ovviamente date da:
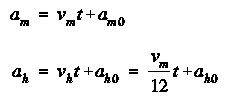
In queste relazioni, am
ed ah sono gli angoli formati dalle due
lancette con una direzione di riferimento prefissata,
mentre am0 e ah0 sono i valori di
tali angoli al momento iniziale della nostra osservazione
(quando t=0).
Per semplificarci la
vita, ma senza perdere alcunché in generalità, possiamo
supporre che l’istante iniziale corrisponda esattamente a
mezzogiorno (o mezzanotte), quando le due lancette sono
perfettamente sovrapposte, e convenire di misurare gli
angoli proprio a partire dalla direzione delle ore
dodici; in questo modo evidentemente le due relazioni
divengono:
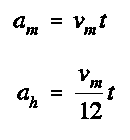 |
(*) |
In
particolare, se l’orologio è esatto, le due velocità
angolari valgono rispettivamente vm=6°/min
per la lancetta dei minuti e vh=0,5°/min per
quella delle ore e quindi:
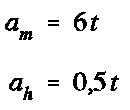
Le leggi del moto ci
consentono non solo di risolvere il problema ma anche di
dominare completamente la situazione. Possiamo per
esempio chiederci dopo quanto tempo dall’inizio
dell’osservazione le due lancette si trovano per la prima
volta in posizione ortogonale oppure contrapposte una
all’altra; le risposte si trovano semplicemente
risolvendo le equazioni:
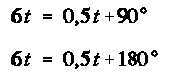
da cui, rispettivamente,
t=16 minuti e 22 secondi circa e t=32 minuti e 44 secondi
circa.
Per venire al nostro
problema, la risposta alla mia domanda
“preliminare” viene dall’equazione:
![]()
da cui t=65 minuti e
27 secondi circa.
L’approccio sintetico mi
è stato suggerito dalla grande vittoria della Ferrari di
Schumacher al Gran Premio di San Marino di ieri (2 maggio
1999). Supponiamo che le due lancette siano in gara tra
di loro e ragioniamo come segue: nelle 12 ore che vanno
da mezzogiorno a mezzanotte la lancella dei minuti compie
esattamente 12 giri e quella delle ore esattamente 1
giro; quindi la prima doppia la seconda esattamente 11
volte nel corso della “gara”; poiché la gara
dura 12 ore ed il moto è uniforme, tra un doppiaggio ed
il successivo trascorre un intervallo di tempo dato da 12
ore divise in 11 parti, ovvero 1 ora 5 minuti e 27
secondi circa, come precedentemente trovato.
Veniamo infine
all’orologio della domanda iniziale: evidentemente, se
l’intervallo tra due doppiaggi è di 65 minuti (cioè un
po’ minore di quello di un orologio esatto) allora
l’orologio va un po’ più veloce del dovuto e quindi va
avanti.
Per un calcolo
dettagliato, possiamo partire dalle leggi del moto (*)
nelle quali supponiamo di conoscere l’intervallo di tempo
tra due sovrapposizioni (65 minuti) ma non la velocità
angolare delle due lancette, fermo restando il loro
rapporto 1:12 (determinato dagli ingranaggi
dell’orologio). Possiamo scrivere:
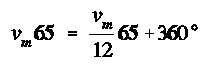
da cui ricaviamo vm=6,042°/min
(contro i 6°/min dell’orologio esatto). Nell’arco di
un’ora, la lancetta dei minuti dell’orologio della
domanda copre quindi un angolo di 362,52°; un orologio
esatto impiega 1 ora e 25 secondi per coprire lo stesso
angolo, quindi il primo orologio va avanti di 25 secondi
ogni ora, ovvero 10 minuti al giorno.