L’esperimento cui si fa riferimento nella domanda e’ quello descritto
nella pubblicazione di Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred
Eibl, Harald Weinfurter & Anton Zeilinger, Experimental Quantum Teleportation,
Nature vol.390, 11 Dec 1997, pp.575.
I propositori di questo approccio sono stati sei scienziati C.H. Bennett,
G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters, “Teleporting
an Unknown Quantum State via Dual Classical and EPR Channels“, Phys.
Rev. Lett. vol. 70, pp 1895-1899 (1993) che hanno pensato un modo per
trasmettere l’intera informazione contenuta nello stato quantico di un
oggetto da un luogo ad un altro (ricostruendo fedelmente l’oggetto) senza
violare il principio di indeterminazione di Heisenberg.
Come si vedra’ bene in seguito, questo procedimento non permette di clonare
all’infinito un oggetto, in quanto l’originale viene distrutto proprio
per permettere che tutta l’informazione contenuta in esso possa essere
trasferita. Qui di seguito cerchero’ di spiegare in termini un po’ semplificati
(e non sempre rigorosi) l’idea che sta alla base dell’esperimento, in
modo da capire se si possano applicare o no gli stessi principi ad altri
sistemi fisici diversi dai fotoni.
In ogni caso chi volesse approfondire l’argomento (e siete invitati a
farlo!) puo’ trovare sulla rete diverso materiale interessante. Ecco un
elenco dei siti che ho visitato (ma ce ne sono anche molti altri)
http://www.aip.org/enews/physnews/1997/split/pnu350-1.htm
http://www.cco.caltech.edu/~qoptics/teleport.html
http://www.dfi.aau.dk/amo/qoptics/home.htm
http://www.uibk.ac.at/c/c7/c704/qo/photon/_teleport/tpbsa.html
Oppure potete cercare su un motore di ricerca i termini “quantum + teleportation”.
Inoltre, si puo’ fare riferimento al numero di Aprile 2000 di Scientific
American, su cui inoltre si trova una interessante discussione sulla possibilita’
e sul significato di teletrasportare oggetti macroscopici (ad esempio,
cosa puo’ significare “teletrasportare una persona”? si teletrasportano
anche i “pensieri”? e via di questo passo).
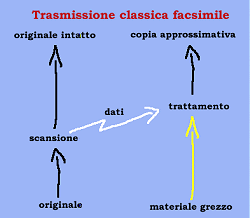
Cominciamo dall’esprimere a parole (in modo molto semplicistico!) cosa
si e’ ottenuto dall’esperimento in questione: un fotone e’ stato teletrasportato
da un posto ad un altro. Per capire quindi cosa sta accadendo e perche’
accade bisogna quindi sapere cos’e’ un fotone (come si comporta, come
viene descritto) e dare la definizione di “teletrasporto”. Cominciamo
dalla seconda cosa. Qui teletrasporto viene inteso nel modo seguente:
l’oggetto originale (qui, il fotone) viene “distrutto” nel luogo in cui
si trova e “ricreato” altrove “nello stesso stato quantico”, ovvero viene
ricreato “identico” all’oggetto che e’ stato distrutto. Vediamo allora
di precisare un po’ meglio il significato di “distruggere”, di “stato
quantico” e via di seguito. Chi avesse gia’ familiarita’ con la meccanica
quantistica, puo’ saltare la parte introduttiva.
Nel caso in esame abbiamo a che fare con il problema di voler trasferire
un sistema quantistico (nel nostro caso un fotone) da un luogo all’altro,
e lo vogliamo fare in modo accurato, lo stato del sistema dopo il trasferimento
deve essere “uguale” allo stato prima. E’ evitente che, per non scontrarsi
col principio di indeterminazione di Heisenberg, non bisogna tentare di
sondare invasivamente il sistema quantistico da teletrasportare in modo
da estrarne informazioni (perche’ in ogni caso il sistema ne risulterebbe
disturbato e sarebbe impossibile risalire a tutta l’informazione in esso
contenuta).
L’idea chiave sta in un’altra caratteristica peculiare della meccanica
quantistica, l'”entanglement“. Il termine “entanglement” fu introdotto
per la prima volta da Schrodinger nella discussione dei fondamenti della
meccanica quantistica. Viene anche detto “correlazione EPR” (Einstein-Podolsky-Rosen)
per un famoso articolo in cui viene discusso. Descrive un sistema costituito
da due o piu’ particelle, che possiede la seguente proprieta’: il risultato
delle misure compiute su una delle particelle costituenti non puo’ essere
specificato indipendentemente dai parametri delle misure sulle altre particelle.
Anche per particelle spazialmente separate il risultato di ciascuna misura
sulla singola particella dipende dallo stato dell’intero sistema, e i
risultati ottenuti sono intimamente collegati l’uno all’altro (e non si
comportano come una collezione di misure raccolte su particelle “che non
si conoscono reciprocamente”, ovvero indipententi tra loro).
Esperimenti che mostrano in modo evidente questo comportamento sono stati
compiuti per la prima volta da Bell negli anni ’60. Ora, sfruttando questa
caratteristica peculiare che possiedono i sistemi quantistici “entangled”
(ovvero quelli “intimamente correlati”) si puo’ finalmente realizzare
un “teletrasporto”, ovvero un sistema che “smaterializzi” il sistema da
teletrasportare da una parte e lo “ricostruisca” fedelmente dall’altra.
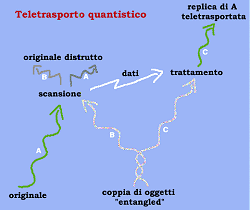
Bisogna per prima cosa avere un sistema “entangled” che sara’ il “vettore”
dell’informazione da un luogo all’altro (dal momento che, ripeto, questi
sistemi hanno la peculiarita’ di mantenere l'”accoppiamento” reciproco
anche a distanza). A questo punto bisogna provvedere a “mescolare” il
sistema da teletrasportare con una delle due “parti” del sistema “entangled”,
compiere una misura di qualche sorta (con cui in realta’ si va a distruggere
lo stato originale). Dal momento che la misura ha coinvolto una delle
due parti di un sistema “entangled”, allora una opportuna misura fatta
sulla altra parte (ovvero dipendente dal tipo di misura fatta sulla prima
parte del sistema E dai suoi risultati) portera’ alla ricostruzione perfetta
dell’oggetto originale da teletrasportare, in quanto la parte rimanente
del sistema “entangled” viene a possedere (proprio per questa sua caratteristica)
le informazioni necessarie per la ricostruzione dell’oggetto originale.
Cio’ e’ stato fatto ad Innsbruck per fotoni, ma e’ chiaro che potendo
disporre di un sistema “entangled” opportuno, in linea di principio cio’
puo’ essere fatto anche per particelle massive. La cosa cruciale e’ proprio
poter disporre di un sistema “entangled” opportuno per l’oggetto da trasportare,
e fare in modo che questo sistema non interagisca con altri oggetti “strada
facendo” e mantenga il suo carattere di “entangled”. Come si puo’ ben
vedere, per ora il problema del teletrasporto di corpi macroscopici e’
un traguardo lontanissimo.
Definizione di stato quantico
e prevedere il “comportamento fisico” della realta’ (anche questa
e’ una spiegazione un po’ frettolosa). La meccanica quantistica
(nel seguito: QM) e’ quella parte della fisica che descrive in modo
appropriato il comportamento dei sistemi “quantistici”, ovvero quella
parte di sistemi (su scala “microscopica”) su cui le previsioni
della meccanica classica (nel seguito: CM) falliscono. Esempi “lampanti”
di sistemi che necessitano di una descrizione quantistica sono gli
atomi (classico il modello dell’atomo di idrogeno) per poter spiegare
le peculiarita’ dei legami chimici, degli spettri atomici etc etc.
Si ricordera’ che in CM lo stato di un sistema ad un certo istante
t e’ determinato fissando a quell’istante il valore delle coordinate
che lo descrivono e delle relative derivate prime temporali (oppure
delle variabili canoniche o dei loro momenti coniugati). Prendendo
ad esempio un sistema composto da N punti materiali nello spazio
tridimensionale, le coordinate che descrivono il sistema sono le
tre coordinate della posizione di ciascun punto materiale e le tre
componenti della velocita’. Fissando il valore di tutte queste 6*N
variabili, si ottiene lo stato del sistema. A partire da queste
informazioni se ne possono ricavare molte altre, come ad esempio
l’energia cinetica del sistema, la sua energia totale (occorre conoscere
il tipo di interazione tra i componenti elementari del sistema),
il momento angolare totale, la posizione del centro di massa e cosi’
via.
Analogamente a quanto si fa in CM, in QM lo stato del sistema viene
detto “stato quantico”, e invece di essere una “collezione” di coordinate
e velocita’ per ciascun istante consiste invece in una funzione
complessa, ovvero una funzione ad ogni punto di un certo spazio
di partenza associa un numero complesso. Spesso tale funzione viene
indicata come “funzione d’onda” del sistema (1).
possiamo scegliere come spazio di partenza lo spazio tridimensionale
(su questo punto non mi dilungo, ma c’e’ parecchio da dire (rappresentazione
nello spazio delle coordinate, rappresentazione nello spazio degli
impulsi…).
Dalla conoscenza di tale funzione, si possono ottenere diverse informazioni
sul sistema (anzi, si puo’ dire che nella funzione d’onda siano
contenute le informazioni per sapere come risponde o rispondera’
il sistema a tutti gli esperimenti che verranno compiuti su di lui!).
Ad esempio, il modulo quadro della funzione d’onda ad un certo istante
t e’ una densita’ di probabilita’. Piu’ precisamente, fissato un
punto nello spazio, il valore del modulo quadro della funzione d’onda
ad un certo istante moltiplicata per il volume di un cubetto infinitesimo
di spazio attorno al punto fissato, e’ pari alla probabilita’ di
trovare l’elettrone in quel cubetto di spazio all’istante fissato.
Inoltre, e’ possibile calcorare il valor medio delle grandezze fisiche
di interesse sullo stato quantico assegnato “mediando” sullo stato
quantico l’operatore quantistico legato alla grandezza fisica che
si vuole esaminare. In base alla conoscenza dello stato quantico
(ovvero della funzione d’onda) si puo’ prevedere (in probabilita’)
il risultato della misura di una grandezza fisica del sistema (di
un osservabile). Il problema delle “misure” e’ di cruciale importanza
in QM. Infatti, ogni volta che viene compiuta una misura il sistema
viene “disturbato” e non c’e’ nessuna garanzia che rimanga nello
stato in cui si trovava prima della misura. Inoltre esistono grandezze
fisiche che non e’ mai possibile misurare contemporaneamente (osservabili
non compatibili). Per tali grandezze fisiche risulta impossibile
rendere piccola a piacere ognuna delle incertezze con cui si conoscono
i valori medi delle grandezze. Il principio di indeterminazione
di Heisenberg quantifica questa importantissima carattesistica intrinseca
dei sistemi quantistici: dati due osservabili incompatibili, fornisce
un limite inferiore per il prodotto delle incertezze sul valor medio
di ciascun osservabile. Si vede quindi che se il prodotto di due
oggetti ha un limite inferiore e uno dei due oggetti e’ molto piccolo,
allora l’altro sara’ necessariamente maggiore di una quantita’ grande.
Il principio di indeterminazione di Heisenberg non puo’ mai essere
violato, in quanto e’ una caratteristica intrinseca del “comportamento
quantistico”. Un esempio di osservabili incompatibili sono la posizione
e la quantita’ di moto di una particella. E’ ben noto che quando
la posizione e’ nota con grande accuratezza, l’incertezza sulla
velocita’ (proporzionale alla quantita’ di moto) e’ molto grande
e viceversa. Per questi due osservabili vale la relazione
DX * D Px
>= 1/2 h/(2*Pi greco)
h e’ la costante di Planck (Volendo, sulla rete si puo’ dare un’occhiata
alla pagina http://www.quipo.it/atosi/numero2/heisenberg/sommario.htm
ed ai link in essa contenuti. Ancor meglio sara’ guardare un buon
testo di meccanica quantistica.
Note:
(1) il nome “funzione d’onda” e’ legato
al fatto che l’equazione fondamentale per l’evoluzione temporale
in QM e’ l’equazione di Schrodinger
i d(Psi)/dt = H Psi
Psi=funzione di t e della posizione, che per gli autostati di una
hamiltoniana indipendente dal tempo comporta una dipendenza temporale
della funzione del tipo Exp(iwt), tipica di oggetti “ondulatori”.
Ancora meglio: la novita’ (e quindi la miglior efficacia nello spiegare
il “funzionamento” della realta’) della meccanica quantistica rispetto
a quella classica sta anche nel fatto che riesce a spiegare il comportamento
“ondulatorio” della materia (interferenza degli elettroni che passano
attraverso due fenditure, etc etc). La descrizione dell’elettrone
mediante funzioni d’onda permette di giustificare molto bene comportamenti
quali l’interferenza, la diffrazione etc, tipici delle onde. Per
maggiori dettagli vedere un buon libro sugli esperimenti “storici”
della meccanica quantistica.