Si può provare
sperimentalmente che la regola ora trovata vale anche
se il recipiente ha una forma qualsiasi, non cilindrica.
Si prendano tre recipienti che abbiano la stessa base
ma forme diverse (vedi figura); ognuno di essi abbia il
fondo costituito di una lamina di gomma. Se in questi tre
recipienti si versa una certa quantità di acqua, le
membrane del fondo, per azione della pressione esercitata
dal peso dell’acqua, si gonfiano. Ebbene, si vede che,
quando l’acqua raggiunge nei tre recipienti la stessa
altezza, le tre membrane si gonfiano egualmente; il che
indica che le pressioni sui fondi dei tre recipienti
hanno lo stesso valore.
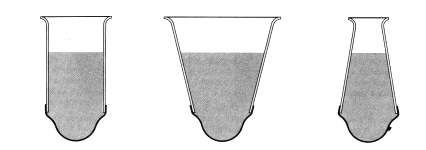
Figura 1. In questi
tre recipienti, che sono riempiti tutti fino allo stesso
livello, la pressione sul fondo è la stessa; infatti, le
tre membrane elastiche, sostituite ai fondi dei
recipienti, si deformano egualmente.
Quindi, nell’enunciare
la regola precedente, si può prescindere dalla
particolare forma del recipiente e dire, in generale,
che: in un liquido pesante, ogni strato orizzontale è
sottoposto a una pressione (pressione idrostatica)
il cui valore è dato dal prodotto del peso
specifico del liquido per il dislivello fra lo strato
considerato e la superficie libera del liquido (legge
di Stevino).
Le seguenti
considerazioni permettono di giustificare che la
pressione di un liquido dipende soltanto dal livello che
esso raggiunge nel recipiente e non dalla forma di
questo. Supponiamo che nei tre recipienti (a), (b), (c)
lo stesso liquido raggiunga lo stesso livello (vedi le
tre figure successive). Per effetto della pressione del
liquido, sulle pareti dei recipienti si esercitano forze
ad esse perpendicolari e rivolte dal liquido verso le
pareti.
Per il principio di
azione e reazione, le pareti esercitano sul liquido forze
eguali ed opposte a queste: siano F, F’
e F”. Perché il liquido sia in equilibrio,
è necessario che la risultante di queste forze sia
eguale ed opposta al peso del liquido.
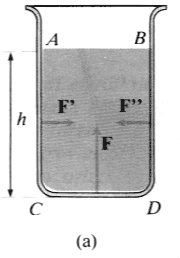 |
Nel caso del recipiente (a), le forze F’ e F” sono orizzontali, perché le pareti sono verticali; invece la F è verticale e rivolta verso l’alto. Poiché F’ e F” si fanno equilibrio, la sola forza F deve equilibrare il peso del liquido. In questo caso, dunque, tutto il peso del liquido è sorretto dalla resistenza della base; e la forza che si esercita sul fondo è eguale al peso della colonna liquida di sezione eguale alla base del recipiente e di altezza h. |
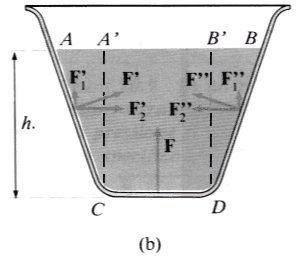 |
Nel caso del recipiente svasato (b), F’ e F” sono rivolte obliquamente verso l’alto. Ciascuna di esse può essere decomposta in una componente orizzontale (F2’ e F2“), che non sorregge il peso del liquido, e in una componente verticale (F1’ e F1“) rivolta verso l’alto. Queste due componenti verticali sorreggono una parte del peso del liquido: precisamente si può dimostrare che esse fanno equilibrio ai pesi delle porzioni di liquido AA’C e BB’D sovrastanti le pareti laterali. La base del recipiente sorregge dunque, anche in questo caso, il peso di una colonna liquida cilindrica avente altezza h e base pari alla base del recipiente. |
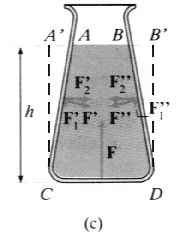 |
Infine, nel caso del recipiente (c), ristretto verso l’alto, le componenti verticali delle F’ e F” sono rivolte obliquamente verso il basso. Quindi la forza F, esercitata dalla base, deve fare equilibrio non soltanto al peso del liquido ma anche alle due forze verticali F1’ e F1“, le quali sono eguali al peso che avrebbero i volumi di liquido AA’C e BB’D che si dovrebbero aggiungere al recipiente per farlo diventare cilindrico. Anche in questo caso, dunque, il peso sorretto dalla base è eguale al peso di una colonna liquida cilindrica, avente altezza h e base pari alla base del recipiente. |