Il problema della codifica delle stringhe binarie è nato all’inizio
degli anni ’70, proprio per progettare i supporti di archiviazione ottici.
Il processo di scrittura su supporto ottico è assimilabile ad un processo
di codifica di un segnale sorgente binario in cui avviene,
contestualmente, compressione del segnale.
Si supponga di voler registrare su supporto ottico la stringa di binaria
di n bit
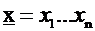, dove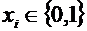 
Al termine del processo di scrittura, che introduce necessariamente
errori, alcuni dei bit della stringa originale verranno alterati. Si supponga
che la probabilità di alterare un bit, a prescindere dalla sua posizione
sia p < ½, da cui, per contro, la probabilità di non alterarlo
sia (1-p).
La registrazione su supporto ottico corrisponde quindi a sommare una
stringa
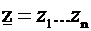, dove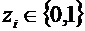 
che ha k bit alterati con probabilità pk, da
cui l’espressione che determina la probabilità della stringa z:
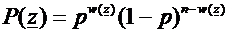
ove w(z) è il cosiddetto peso della stringa z,
ovvero il numero di 1 che essa contiene. La probabilità di z si
calcola facilmente osservando che per ogni 1 interviene un termine di probabilità
p e per ogni zero uno di probabilità (1-p), mentre se w(z)
è il numero di 1, n – w(z) è il numero di 0.
In un CD, le stringhe binarie vengono scritte a lotti di n bit,
solitamente 16, ma n può essere variato a piacimento in base al
sistema di codifica; essendo un CD assimilabile ad una stringa binaria
praticamente infinita (circa 108 bit), per esso vale la legge
dei grandi numeri, ovvero il numero di errori medio che si commette
nella registrazione è np, ovvero:
All’atto della scrittura su CD, si somma in XOR una stringa z
all’originale della sorgente x, il che equivale a dire che si ottiene
una nuova stringa y :
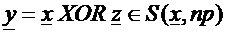
ove S(x, np) è detta sfera di centro
x e raggio np, ottenuta alterando np bit della stringa
x di partenza.
Qualsiasi sistema di decodifica, per essere affidabile, deve sempre
consentire di ricostruire la stringa x originale, a partire dalla
stringa y registrata sul supporto, altrimenti si avrebbe fenomeno
detto di aliasing, ovvero una decodifica inversa che non restituisce
l’originale.
Ciò significa che qualsiasi sistema di decodifica deve garantire la
non intersezione delle sfere di appartenenza delle stringhe dopo il processo
di decodifica, ovvero:
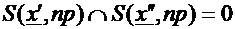, per ogni x‘,
x”.
Stabilire un codice vuol dire, quindi, identificare un set di stringhe
non confondibili, centri delle sfere in cui cade il segnale dopo la codifica.
Il problema principale è stabilire la miglior codifica possibile, ovvero
far si che il codice C, composto dalle stringhe non confondibili,
copra tutto lo spazio S dei segnali da codificare:
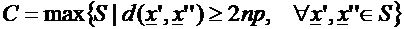
ove d è la distanza in bit tra due stringhe.
La capacità di correzione di errore di un codice è direttamente
legata alla cardinalità del codice stesso, ma in modo asintotico:
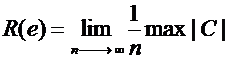
relazione che esplicita la capacità di correggere errori in un codice
di cardinalità |C|. Si dimostra che un codice caratterizzato da capacità
di correzione R(e) garantisce nR(e) bit detti “liberi”, destinati
ad ospitare il controllo di ridondanza per la correzione di e/2 errori.
In soldoni, riducendo la cardinalità del codice C, ovvero aumentando
il passo di compressione, ci si scontra inevitabilmente con l’incapacità
di riprodurre il segnale originale.
Si dimostra che R(e) è limitato superiormente ed inferiormente
(per e < ½) dalle disuguaglianze di Gilbert-Varshamov ed Hamming:
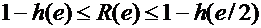
dove h è l’entropia binaria del segnale, definita come h
= -(p log2 p+ (1-p) log2
(1-p)).
L’entropia rappresenta, praticamente, il grado di caoticità del segnale
in ingresso che, ricordiamo, è costituito da sequenze di 0 e 1. Il massimo
dell’entropia si ha per p = ½, ovvero quando le stringhe sono composte
indifferentemente da 0 e da 1, mentre il minimo dell’entropia si ottiene
quando si tende ad avere lunge sequenze di 0 o 1.
Si dimostra, ancora, che l’entropia del segnale concorre a determinare
non solo il tasso di errore, ma anche la lunghezza media della stringa
ottenuta dopo la codifica, ovvero:
|y| = nh(p)
Riassumendo, l’entropia del segnale in ingresso determina:
- La capacità di correggere errori.
- La dimensione massima di compressione.
Nel caso di un CD musicale, comprimere eccessivamente vuol dire quindi
perdere in capacità di correggere errori e, quindi in qualità.
La tabella che segue illustra una stima del livello di compressione
attuabile su stringhe di 16 bit:
|
p |
0 |
1 |
H(p) |
nH(p) |
|
0,1 |
14,4 |
1,6 |
0,47 |
7,50 |
|
0,2 |
12,8 |
3,2 |
0,72 |
11,55 |
|
0,3 |
11,2 |
4,8 |
0,88 |
14,10 |
|
0,4 |
9,6 |
6,4 |
0,97 |
15,54 |
|
0,5 |
8 |
8 |
1,00 |
16,00 |
|
0,6 |
6,4 |
9,6 |
0,97 |
15,54 |
|
0,7 |
4,8 |
11,2 |
0,88 |
14,10 |
|
0,8 |
3,2 |
12,8 |
0,72 |
11,55 |
|
0,9 |
1,6 |
14,4 |
0,47 |
7,50 |
La prima colonna riporta la probabilità che un carattere della stringa
binaria sia pari 1, la seconda il numero di 0 e di 1 rispettivamente attesi
per quella probabilità, la quarta riporta il valore corrispondente dell’entropia
binaria e l’ultima colonna il numero di bit medi per rappresentare il segnale
avente probabilità p.
Si osservi che l’entropia è massima e pari ad uno solo se 0 ed 1 sono
equiprobabili: in questo caso è impossibile comprimere senza perdita di
informazione. Se il numero di 0 o 1 scende, ad esempio se su una stringa
di 16 bit sono quasi tutti 0, allora il codice può fornire una rappresentazione
senza perdita di informazione usando meno di 8 bit.
Fermo restando che il progresso della scienza è inarrestabile, fino
a sconfinare nella magia – come diceva Arthur C. Clarke – appare quindi
estremamente azzardato affermare che si può ridurre un segnale binario
dell’ordine di 108, fino a pochi kb, quindi di un’ordine di
103 qualsiasi sia il segnale e senza perdita di compressione.