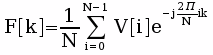La funzione DFT (Discrete Fourier Transform)
è un algoritmo strettamente connesso con la classica trasformata di
Fourier trasportata nel campo “discreto”.
La funzione
FFT (Fast Fourier Transform) non
è altro che una DFT calcolata mediante un algoritmo veloce (Fast).
Queste funzioni hanno la principale applicazione nello studio degli andamenti temporali
di fenomeni effettuato con mezzi digitali.
Dovendo analizzare un parametro che varia nel tempo, il suo valore dovrà
essere campionato, ovvero registrato ad intervalli regolari
e la sequenza di campioni costituiscono i dati di ingresso del problema.
Detto V[i], i=1,..N il vettore contenente la sequenza dei campioni la corrispondente funzione DFT è
definita come:
Senza entrare nel merito delle definizioni formali e dello studio delle trasformate
discrete, possiamo però dire che il risultato dalla DFT
è un vettore della stessa lunghezza del vettore dei campioni,
i cui elementi
si possono interpretare come le componenti periodiche (o “spettrali”)
dell’andamento temporale del fenomeno osservato.
Ovvero il fenomeno viene interpretato come la composizione di singole componenti
sinusoidali a diverse frequenze combinate linearmente fra loro. I valori
risultanti dalla DFT sono i coefficienti della combinazione
lineare1.
Il termine di indice 0 (il primo del vettore risultante) è quello connesso alla componente
a frequenza 0 (ovvero alla parte costante del fenomeno osservato). Quando tale
valore è diverso da zero significa solamente che il fenomeno non
è a media nulla. Questo nel caso, ad esempio, di segnali elettrici si traduce nel fatto che la
“componente continua” è diversa da zero.
A titolo di
esempio mostriamo una simulazione di un fenomeno molto semplice
ottenuto
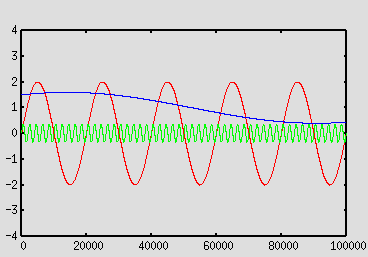
sommando fra loro tre funzioni periodiche (sinusoidali). Nelle seguenti
figure
sono mostrate le tre funzioni (Figura 1) e la funzione risultante dalla
loro somma
(Figura 2, f1 (tratto rosso)). Sempre in Figura 2, con tratto verde,
viene mostrata una seconda
funzione f2, ottenuta dalla f1 sottraendo il valore medio. La funzione
f2 ha quindi esattamente le stesse componenti periodiche di f1, ma ha
media nulla.
 |
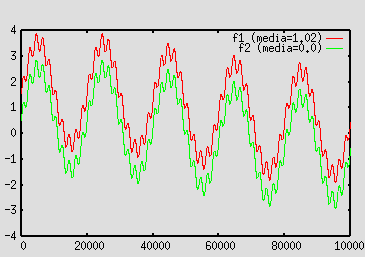 |
| Figura 1 – Componenti dei segnali | Figura 2 – Segnali da analizzare (f1, f2) |
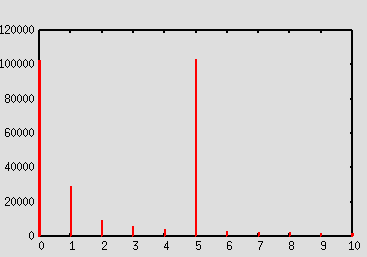
Nelle Figure 3 e 4 sono mostrate le prime componenti2
delle funzioni DFT
calcolate rispettivamente sulla funzione f1 ed f2. È evidente come l’unica
differenza sia rappresentata dal valore della componente di indice 0.
 |
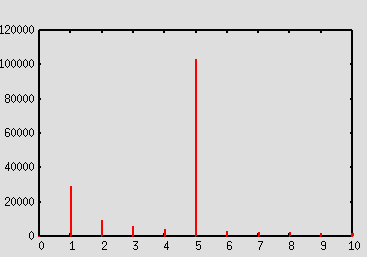 |
| Figura 3 – DFT(f1) | Figura 4 – DFT(f2) |
Spesso avendo calcolato la DFT di un segnale, si utilizza un vettore le
cui componenti sono calcolate come il quadrato del modulo delle
componenti della DFT. Tale vettore è chiamato “spettro di potenza”
del segnale e corrisponde alla percentuale della potenza complessiva del
segnale derivante da ciascuna componente spettrale3.
(1) Le cose sono in realtà più complesse (nel
vero senso della parola) in quanto la DFT è in generale un vettore a valori
complessi da cui è possibile ricavare ampiezza e fase della componente relativa.
(2) Tutte le componenti successive non mostrate nel grafico
sono nulle, perché il segnale è la somma di tre sole componenti
periodiche e nella DFT mancano quindi i termini a frequenze più alte.
(3) I valori mostrati nei grafici delle figure 3 e 4
sono in realtà lo spettro di potenza delle rispettive DFT.