Un segnale aleatorio (o processo aleatorio) è una funzione del tempo in cui ad ogni istante il valore è una variabile aleatoria. Se le caratteristiche della variabile aleatoria non cambiano nel tempo il processo è detto stazionario e si possono definire grandezze del primo ordine come media e varianza del processo che non dipendono dal tempo.
In generale è utile definire grandezze di ordine superiore, cioè che dipendono dalla distribuzione di probabilità congiunta delle variabili aleatorie corrispondenti a istanti diversi. Ad esempio l'autocorrelazione di un processo è definita come:
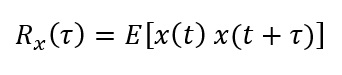
in cui il valore atteso E() è una media di insieme, cioè si riferisce a tutte le possibili realizzazioni del processo. Se il processo è stazionario l'autocorrelazione non dipende da t ma soltanto da τ.
Una classe particolare di processi stazionari è quella dei processi ergodici per i quali le medie di insieme sono uguali alle medie temporali di una sola realizzazione, in pratica una singola realizzazione è rappresentativa di tutto il processo. Allora la funzione di autocorrelazione si può calcolare come media nel tempo:
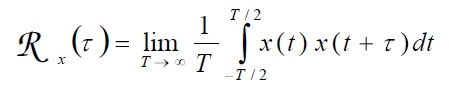
Lo spettro di densità di potenza si può calcolare con la trasformata di Fourier della funzione di autocorrelazione.
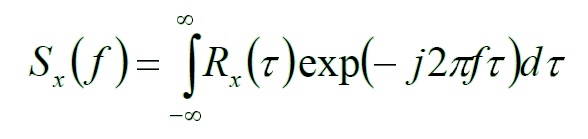
Tuttavia è necessario fare alcune riflessioni prima di applicare queste formule.
Innanzi tutto l'ambito di studio, la sismica. Il "segnale" (o meglio la terna di segnali, uno per ogni asse cartesiano) registrato da un sismografo durante un terremoto può sembrare benissimo una "realizzazione" di un processo aleatorio. Nella figura sono riportati i sismogrammi della scossa del 29 Maggio 2012 che ha colpito la provincia di Modena causando molti danni e decine di vittime. (Immagini dal sito Orfeus: Observatories and Research Facilities for European Seismology)
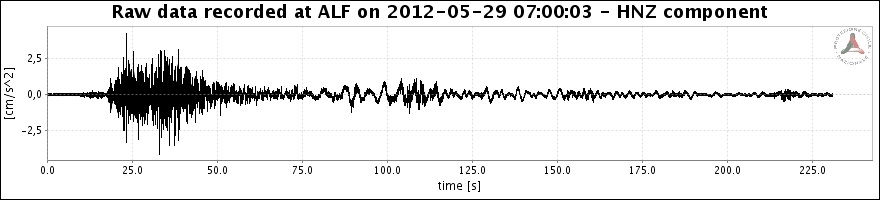
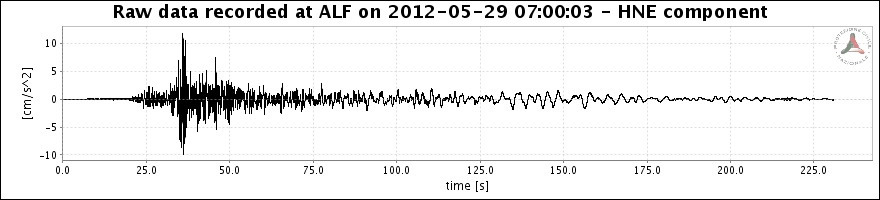
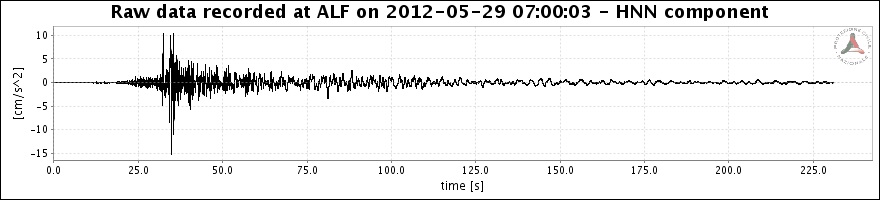
Già ad una prima occhiata però sorge il dubbio che il processo non sia stazionario perché si vede subito che le onde iniziano con un picco e poi sono smorzate.
Questo complica la stima dello spettro di densità di potenza. Tuttavia è possibile eseguire la trasformata di Fourier. Trattandosi di un segnale campionato si può utilizzare la trasformata di Fourier discreta (DFT) o la sua versione più efficiente (FFT).
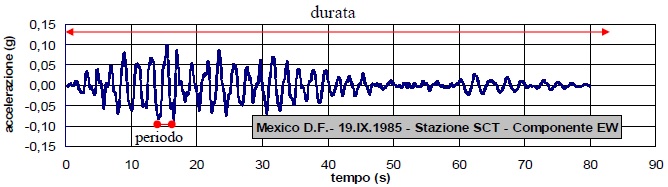
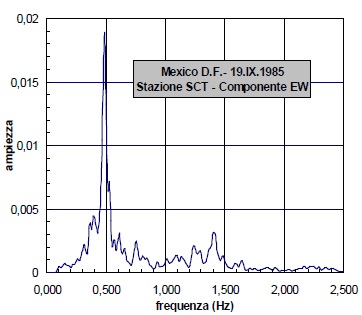
Ad esempio nella figura seguente è riportata la forma d'onda di un evento sismico del 1985 in Messico e la sua trasformata di Fourier. Si può notare che lo spettro indica una grande componente a frequenza 0,5Hz, e questo si può ritrovare nella forma d'onda osservando che in un intervallo di 10s ci sono circa 5 oscillazioni complete.
Ricordiamo due utili proprietà della trasformata di Fourier discreta:
– la risoluzione in frequenza dello spettro è pari all'inverso della durata del segnale
– l'estensione di banda della trasformata è data dall'inverso dell'intervallo di campionamento
Nel caso del sismogramma dell'Emilia del 2012 si può notare che il contenuto frequenziale è diverso tra l'inizio e la fine dell'evento, in parte perché arrivano prima le onde P (di pressione) e poi le onde S (di taglio) e poi perché c'è una lunga coda di onde riflesse e rifratte le cui componenti ad alta frequenza sono attenuate di più di quelle a bassa frequenza. In questi casi può essere utile definire uno spettrogramma, cioè una trasformata di Fourier fatta per settori di diversi intervalli temporali.
Naturalmente poiché le durate degli intervalli da trasformare secondo Fourier sono più brevi dell'intero segnale lo spettro avrà una risoluzione minore.
In questa altra figura è riportato un evento sismico recente e meno drammatico insieme ai sismogrammi di una serie di stazioni in tutta l'Europa.
.jpg)
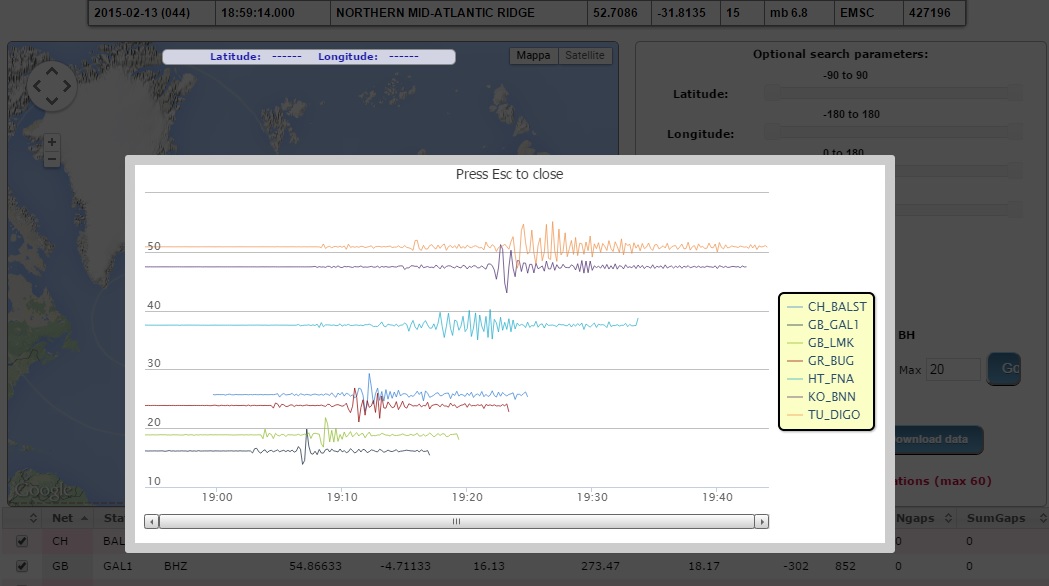
Come si vede chiaramente le stazioni più lontane registrano l'evento con un ritardo maggiore. Anzi è proprio il tempo di ritardo a consentire – dato un certo numero di registrazioni – la localizzazione precisa dell'ipocentro del terremoto. E per questo la correlazione assume un significato importante, infatti è una tecnica molto accurata per misurare il ritardo tra due segnali, mentre l'autocorrelazione di un segnale in sé ha una scarsa utilità pratica.
Naturalmente nella realtà gli scienziati si trovano a dover affrontare problemi ben più complessi, infatti il segnale sismico registrato da due stazioni lontane è anche molto diverso a causa della trasformazione (attenuazione, dispersione e distorsione) che subisce attraversando i vari strati della terra, e proprio lo studio dei terremoti ha contribuito allo sviluppo di modelli della struttura terrestre.
Alcune informazioni sulla correlazione e sui processi si possono trovare anche in quest'altra risposta di Vialattea e nei suoi riferimenti