Bisogna fare attenzione all’utilizzo dei termini in geometria, e più in generale in matematica. Infatti il loro significato può essere diverso da quello che intendiamo nella lingua di tutti i giorni. In particolare, cosa si intende per ellittico quando si parla di uno spazio?
Per cominciare, conviene fare un parallelo in due dimensioni. Prendiamo per esempio una superficie piana, come un foglio di carta, e consideriamo alcuni enti geometrici che si possono costruire all’interno di questo piano. Consideriamo per esempio dei triangoli: come ci hanno insegnato a scuola, la somma dei loro angoli interni sarà sempre pari a 180°. Similmente, se consideriamo dei cerchi, il rapporto tra la loro circonferenza ed il diametro sarà sempre pari alla costante π ≈ 3.14159… (pi greca). Queste proprietà ci possono sembrare scontate, e sono note fin dall’antica Grecia, ma, dal punto di vista matematico, sono dimostrabili se si accetta un certo numero di assiomi, ovvero affermazioni elementari non dimostrate, né dimostrabili, ma assunte a priori (i cosiddetti postulati di Euclide). Ebbene, come fu capito attorno alla seconda metà del XIX secolo, non è obbligatorio prendere per veri questi assiomi: si possono infatti creare delle geometrie autoconsistenti (cioè senza contraddizioni logiche interne) anche eliminandone alcuni. Queste geometrie sono, naturalmente, differenti da quella che percepiamo attraverso i nostri sensi e che sembra valere per lo spazio in cui esistiamo.
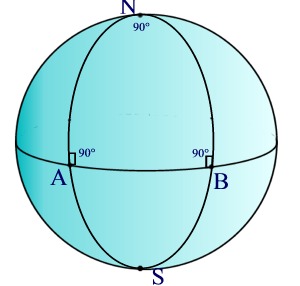 Per visualizzare un po’ meglio questo concetto, facciamo un esempio di geometria non-euclidea, cioè una geometria in cui non valgano tutti i postulati di Euclide. Senza dover considerare nulla di stravagante, si tratta semplicemente della superficie di una sfera. Cerchiamo di costruire un triangolo contenuto strettamente all’interno di questa superficie (si veda la figura a fianco, tratta da www.matematicamente.it), badando bene che non si può uscire dalla "buccia". I lati del triangolo dovranno essere curvi, per esempio possiamo considerare un quarto di equatore (AB) e i due semimeridiani che giungono fino al polo (AN e BN). È molto semplice notare che ciascun angolo di questo triangolo è retto, per cui la somma dei tre angoli è pari a 270°, e non 180°! Si vede come questa geometria è intrinsecamente diversa dalla geometria piana.
Per visualizzare un po’ meglio questo concetto, facciamo un esempio di geometria non-euclidea, cioè una geometria in cui non valgano tutti i postulati di Euclide. Senza dover considerare nulla di stravagante, si tratta semplicemente della superficie di una sfera. Cerchiamo di costruire un triangolo contenuto strettamente all’interno di questa superficie (si veda la figura a fianco, tratta da www.matematicamente.it), badando bene che non si può uscire dalla "buccia". I lati del triangolo dovranno essere curvi, per esempio possiamo considerare un quarto di equatore (AB) e i due semimeridiani che giungono fino al polo (AN e BN). È molto semplice notare che ciascun angolo di questo triangolo è retto, per cui la somma dei tre angoli è pari a 270°, e non 180°! Si vede come questa geometria è intrinsecamente diversa dalla geometria piana.
Siamo finalmente nella condizione di definire propriamente il termine usato nella domanda: una geometria si dice ellittica quando la somma degli angoli interni dei triangoli costruiti su tale superficie è maggiore di 180°. Nel caso opposto, la geometria si dice iperbolica, mentre quando la somma viene esattamente 180° siamo in corrispondenza di una geometria piatta (non necessariamente piana). Senza addentrarsi in troppi dettagli, si può far vedere che questa ed altre proprietà (come il rapporto tra la circonferenza ed il diametro) sono intrinseche per ogni superficie, e sono legate ad un parametro chiamato curvatura. Per fare un esempio, è noto che non si può adattare una superficie sferica ad una piana senza stirarla o strapparla: questa è una manifestazione che le due superfici hanno curvatura diversa. Al contrario, un cono od un cilindro possono essere "srotolati" e fatti diventare un piano, perché queste due superfici hanno in realtà la stessa curvatura.
Tutto questo preambolo matematico può lasciare un po’ sconcertati… Cosa c’entra con l’Universo? La ragione di queste complicazioni sta nella teoria della Relatività Generale, dovuta ad Albert Einstein, che governa il comportamento dell’Universo nel suo insieme. Questa teoria afferma che lo spazio in cui viviamo non è un semplice "contenitore" di stelle, pianeti, gas e radiazione, ma viene deformato e plasmato dalla materia e dall’energia che contiene. Esattamente come una sfera, lo spazio è pure dotato di curvatura, la cui ampiezza dipende dalla materia al suo interno. Rispetto ad una superficie sferica, ci sono alcune differenze: innanzitutto l’Universo non ha due ma addirittura quattro dimensioni (tre spaziali ed una temporale); in secondo luogo, la curvatura non è costante punto per punto, ma varia spostandosi, in dipendenza della quantità di materia ed energia presenti.
Ma tutto questo non è in contrasto con l’intuizione e con quanto osserviamo ogni giorno? Dopotutto, la geometria euclidea, piatta, sembra funzionare perfettamente per descrivere il nostro Universo. In effetti, l’influenza della materia nell’incurvare l’Universo è estremamente debole, e la curvatura è di solito così piccola che è impossibile accorgersene. Se però si considerano grandi scale (miliardi di anni luce), allora l’effetto della geometria non euclidea diventa fondamentale. La curvatura dello spazio diventa importante anche in presenza di grandi densità, per esempio in vicinanza di buchi neri. Verifiche sperimentali sono state effettuate con successo anche su scale più a misura d’uomo, usando speciali strumenti, ma sulla Terra gli effetti della geometria non piatta dello spazio sono minuscoli.
Dalla discussione impostata sopra, si capisce che il termine ellittico non implica che l’Universo abbia la forma di un’ellisse o di un ellissoide. Affermare che l’Universo è uno spazio ellittico vuol dire che la geometria dell’Universo è ellittica. Uno spazio a geometria ellittica non è necessariamente finito, può anche essere illimitato. Per esempio, se si considera una parabola e la si fa ruotare attorno al proprio asse, si costruisce una superficie cosiddetta paraboloide. Questa superficie è infinita spazialmente ed ha geometria ellittica.
Per concludere, una nota di carattere più fisico. Oggigiorno, la geometria dell’Universo può essere misurata sperimentalmente tramite osservazioni astronomiche. Queste misure sono estremamente complesse, per cui non si possono prendere come oro colato, ma i dati ad oggi disponibili sembrano consistenti con un Universo a geometria piatta, non ellittica. Senza addentrarci in troppi dettagli, faccio riferimento al tutorial di cosmologia ospitato da ViaLattea per ulteriori chiarimenti.
La seconda parte della domanda richiede di esplicitare possibili errori nella concezione dell’Universo. Be’, ovviamente ciascuno è libero di sbagliare quanto e quando vuole! Comunque, uno dei primi passi falsi che si può commettere riguarda proprio l’estensione dell’Universo. Di fatto, ad oggi, non conosciamo quanto è grande, e non sappiamo neppure se è finito oppure infinito. Sappiamo solo che è molto grande. Infatti, dato che sono trascorsi "soltanto" 13 miliardi di anni dal Big Bang, noi possiamo osservare solamente quella parte di Universo che la luce ha potuto percorrere durante questo tempo (a causa dell’espansione dell’Universo, questa distanza non è esattamente 13 miliardi di anni-luce, ma come stima brutale è sufficiente considerare questo numero). Cosa sia oltre questa distanza, non ci è dato sapere. L’universo potrebbe essere illimitato, con infinite stelle e pianeti oppure potrebbe essere finito. Potrebbe addirittura essere chiuso su se stesso, come una circonferenza in cui, procedendo in una direzione, si incontra nuovamente il punto di partenza. Non bisogna neppure pensare che l’Universo fosse "piccolo" nei primi istanti dopo il Big Bang: se l’Universo è infinito al giorno d’oggi, lo è sempre stato. Semplicemente, via via che ci si avvicina al Big Bang, la distanza media tra i punti diventa più piccola, ma i punti rimarrebbero sempre infiniti.