La
complessità computazionale di un algoritmo è definita come l’ordine di
grandezza della funzione che determina il numero di passi elementari da
svolgere per eseguirlo, al crescere della dimensione dei dati di ingresso.
La complessità computazionale,
in questo senso, è quindi una misura di tempo astratta che ha,
al più, una relazione di proporzionalità con il tempo
effettivo di esecuzione.
Si parla anche di complessità
computazionale spaziale, intesa come dimensione della struttura dati necessaria
a supportare l’esecuzione di un algoritmo. Tuttavia, non si dovrebbe associare
la complessità (computazionale) spaziale alla memoria e computazionale
al tempo, poiché in entrambi i casi si sta valutando l’ordine
di grandezza delle quantità associate (tempo e memoria).
L’analisi della complessità
temporale di un algoritmo consente di determinare l’ordine di grandezza
del tempo necessario per eseguirlo senza nemmeno iniziare la computazione.
Questo approccio ha dei vantaggi considerevoli, infatti è possibile
scrivere algoritmi che terminano in un numero considerevole di anni.
Si supponga di scrivere il seguente
algoritmo ricorsivo per il calcolo del fattoriale:
Algoritmo F1:
if n = 0 then
f = 1;
else
f = n*F1(n-1);
e si supponga di voler calcolare
F1(1000) con un calcolatore in grado di fare un miliardo di iterazioni
elementari (o passi) al secondo: occorrerebbero 2551 anni.
L’analisi della complessità
dell’algoritmo F1 consente, quindi, di non dover attendere il risultato
fino al capodanno del 4550.
Le regole di valutazione della complessità
computazionale sono le seguenti:
- Le istruzioni di assegnamento
hanno complessità unitaria. - Le iterazioni di tipo for
i = 1 to n do c hanno complessità n volte la complessità
del corpo dell’iterazione c. - Se un algoritmo contiene istruzioni
condizionali di tipo if … then … else, allora ha complessità
minima, media e massima pari al numero di passi minimo,
medio e massimo necessari allo svolgimento delle istruzioni
condizionali che lo compongono.
Con queste regole siamo in grado
di valutare la complessità computazionale di un algoritmo al crescere
della dimensione dei dati di ingresso.
Si consideri ora l’algoritmo per
il calcolo del fattoriale che segue:
Algoritmo F2:
f = 1;
if n > 1 then
for i = 1 to n do f = f * i;
Ora, applicando le regole di calcolo
della complessità computazionale esposte, si valuti la complessità
degli algoritmi F1 ed F2.
Si scopre che F1 ed F2 impiegano
rispettivamente n! e n+1 passi. Il calcolatore di cui sopra
eseguirebbe, quindi, F2(1000) in un milionesimo di secondo circa.
L’analisi della complessità rivela che l’algoritmo F2 è
nettamente più efficiente di F1.
Ma, ai fini della valutazione dell’efficienza,
ciò che interessa è l’ordine di grandezza delle funzioni
che determinano il numero di passi al crescere di n o, in termini
formali, l’ordine di infinito di queste funzioni.
Ricordiamo che una funzione ha lo
stesso ordine di infinito xn se e solo se ![]() ,
,
per c > 0 constante. Questa proprietà si indica affermando
che “f(x) è O(xn)“
Valutando l’ordine di infinito delle
funzioni che determinano il numero di passi necessari a svolgere un algoritmo
siamo in grado di determinare due cose:
- un criterio di efficienza degli
algoritmi - delle classi di computabilità
di algoritmi
Siano f1(n) ed f2(n)
due funzioni di valutazione di complessità computazionale relativi
agli algoritmi A e B rispettivamente.
- A e B hanno la
stessa efficienza: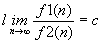 ,
,
con c > 0 constante. - A è più
efficiente di B: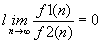
- B è più
efficiente di A: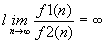
Le classi di computabilità
degli algoritmi vengono invece definite sulla gerarchia di ordini di infinito
delle funzioni di valutazione della complessità computazionale:
- Complessità polinomiale:
algoritmi O(ni) per qualche i - Complessità esponenziale:
algoritmi O(an) per qualche a - Complessità non-polinomiale:
tutti gli altri algoritmi
L’algoritmo F1 è quindi O(n!)
(non-polinomiale), ment