 Fig. 1: La Terra vista dal satellite Apollo 17.
|
Raggio equatoriale 6.378,14 km Raggio polare 6.356,78 km Circonf. equatoriale =40.075,0354 km Circonf. polare =39.940,8267 Km Volume 1,0832 x1012 km3 Massa 5,9737 x 1024 kg Densità 5,515 g/cm3 Area della superficie 510.065.700 km2 Gravità all’equatore 9,766 m/s2 (=1 g) Velocità di fuga 11.180 m/s Periodo di rotazione siderale 23,934 ore Inclinazione assiale 23,45° |
I suoi ambiti d’interesse possono essere suddivisi in due gruppi:
1. Lo studio delle dimensioni e della forma della Terra nella sua globalità e dei suoi aspetti di carattere gravitazionale;
2. Lo studio e la misura di parti della superficie della Terra (topografia).
Tralasciamo la storia degli studi e delle varie elaborazioni succedutesi nei secoli per concentrarci maggiormente sui risultati finali.
Per determinare con esattezza la posizione di un luogo sulla superficie terrestre, bisogna usare lo strumento delle coordinate geografiche: la latitudine e la longitudine.

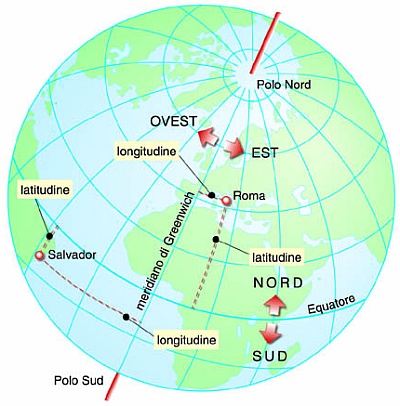
Fig. 3: Rappresentazione di meridiani e paralleli.
La longitudine è la distanza angolare di un punto dal meridiano fondamentale di Greenwich, misurata in gradi (l’unità di misura dell’angolo). Alla misurazione si aggiunge l’indicazione Est oppure Ovest, a seconda che il punto si trovi ad oriente o ad occidente del meridiano fondamentale.
Dalla figura 4 si comprende benissimo che un arco massimo lungo un meridiano comprende uno spazio uguale a parità di distanza angolare uguale. Vale a dire che la distanza chilometrica tra un parallelo e l’altro è sempre la stessa (circa 110,9467 Km) in qualsiasi punto della Terra. Per esempio, se “scendo” dal decimo parallelo Nord fino all’equatore, viaggiando lungo un meridiano, potrò conoscere la distanza percorsa con un semplicissimo calcolo: 110,9467 x 10= 1.109,467 Km.
Insomma, viaggiando lungo una qualsiasi circonferenza polare e assumendo che la terra è completamente sferica, per ogni percorso tra un parallelo e l’altro intercorre la stessa distanza di 110,9467 Km.
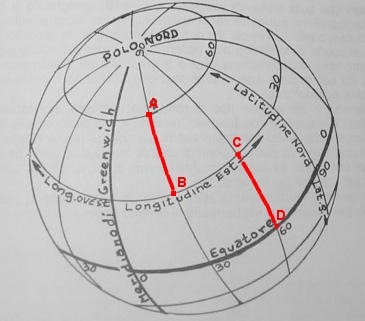
Fig. 4: d(A,B) è la distanza tra A e B; d(C,D) è la distanza in Km tra C e D. Pertanto si ha che d(A,B) = d(C,D) = 110,9467 x 30 =3.328,401 Km.
|
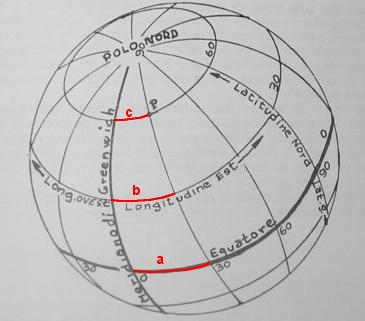 Fig. 5: Appare evidente che i rispettivi percorsi “a”, “b”, “c” differiscono moltissimo tara loro. Perciò la relazione sarà a>b>c.
|
Quindi, passare da un meridiano all’altro a latitudini diverse, implica percorrere distanze diverse (vedi fig. 5).
La risposta è: “Sì, possiamo calcolare la lunghezza dell’arco massimo che unisce due punti qualsiasi della superficie terrestre.”.
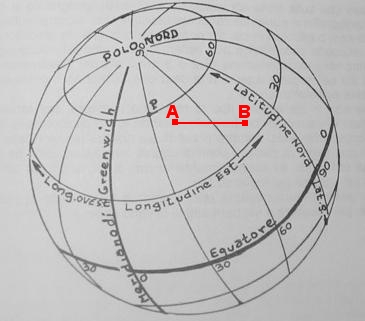
Fig. 6 Due punti qualsiasi.
Siano 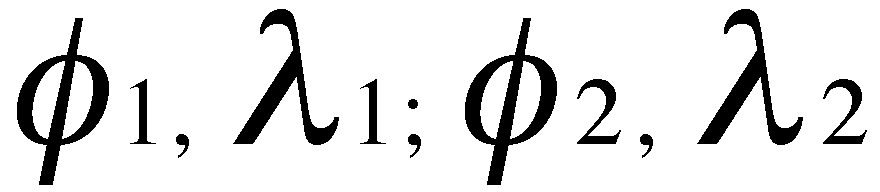 la latitudine (
la latitudine ( ) e la longitudine (
) e la longitudine ( ) rispettivamente dei punti A e B; sia
) rispettivamente dei punti A e B; sia 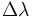 la differenza tra le due longitudini e
la differenza tra le due longitudini e 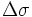 la distanza angolare tra i due punti considerati (A,B),
la distanza angolare tra i due punti considerati (A,B),
la distanza angolare tra A e B è data dalla formula:
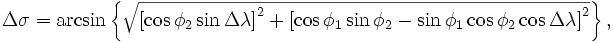
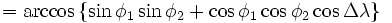
Basta moltiplicare il risultato (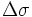 ) x 6360 (raggio della Terra arrotondato) per ottenere la distanza in km.
) x 6360 (raggio della Terra arrotondato) per ottenere la distanza in km.
Con una calcolatrice scientifica o per mezzo di un foglio elettronico sul computer, sarà facile eseguire i calcoli indicati nella formula.
Da aggiungere che in, caso di distanze piccole, la formula qui sopra può fornire un largo errore di arrotondamento. Pertanto, per distanze piccole, dove il coseno è molto vicino a 1 e l’arcocoseno, quindi, poco accurato, è consigliabile utilizzare formule alternative che si possono reperire, assieme a quella qui riportata, al seguente indirizzo:
http://en.wikipedia.org/wiki/Great-circle_distance>http://en.wikipedia.org/wiki/Great-circle_distance
Diversamente, chi non volesse utilizzare la calcolatrice né il foglio elettronico, potrà collegarsi al seguente indirizzo il quale offre la possibilità di tale calcolo dopo aver inserito i parametri richiesti (latitudine e longitudine dei due punti considerati) o due delle principali città mondiali.
http://www.comunedipinasca.it/main.php?section=utility/distanza.php