11 luglio 2005
A questo link potete trovare una versione tipograficamente migliore, con equazioni scritte in Mathjax.
Sul web, ma anche in molti libri di testo, si leggono spesso spiegazioni errate del fenomeno delle maree lunisolari. In particolare risulta erronea la spiegazione dell'esistenza del secondo lobo di marea, quello rivolto in direzione opposta alla Luna. Per spiegare questo fenomeno, infatti, molti autori fanno riferimento alla forza centrifuga, la quale però, essendo una forza fittizia, non può giocare alcun ruolo.
La tesi corretta è che per spiegare le maree sono
necessari e sufficienti gli effetti della differenza della forza di attrazione
gravitazionale tra i punti della superficie terrestre ed il centro della Terra.
La forza centrifuga che appare in molte trattazioni spesso è esposta in modo errato; nei rari casi in cui è trattata correttamente, serve
solo in un sistema di riferimento rotante. E’ quindi un artificio contabile,
senza alcun effetto fisico sulle maree.
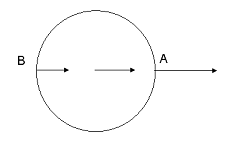
Lo dimostreremo mettendoci in diversi sistemi di riferimento e calcolando l’accelerazione totale per due soli punti di prova: i classici A e B di figura 2, rispettivamente il punto più vicino alla Luna e l'opposto. Se il risultato sarà identico al caso in cui compare la sola forza gravitazionale, potremo stare certi che le forze fittizie non giocano alcun ruolo.
Molta confusione circa le forze di marea nasce infatti dall’uso improprio del sistema di riferimento. Scegliere il sistema di riferimento è il primo passo per affrontare con successo un problema di fisica. Se si compiono errori in questa fase fondamentale, può succedere di tutto. Si possono mescolare concetti appartenenti a diversi sistemi di riferimento, ottenendo mostruosità logiche e fisiche.
Un'altra questione che lascia perplessi è il fatto che per ottenere il campo mareale si deve sottrarre dall'attrazione gravitazionale della Luna un campo uniforme. Fin dal liceo sappiamo bene che in un sistema rotante le forze fittizie sono proporzionali alla distanza dall'asse di rotazione. Quindi, ci chiediamo, da dove scaturisce questo campo uniforme?
Tutto questo sarà svelato negli esempi che seguiranno.
La fisica insegna che ogni situazione reale può essere descritta in modi diversi, a seconda del punto di vista dell’osservatore. Ogni osservatore definisce un proprio sistema di riferimento (SR). Ad esempio, se io sono fermo al bordo di una strada, definirò la strada come il mio SR, mentre se sono dentro un’automobile, mi sarà comodo definire l’automobile stessa come mio SR.
Se l'automobile percorre una curva stretta verso sinistra, l'osservatore solidale alla strada farà il seguente ragionamento:
Per il principio di inerzia il passeggero tende a proseguire il suo moto rettilineo, tuttavia i pneumatici stanno imprimendo una direzione diversa al moto: la macchina curva verso sinistra, andando a comprimere il lato destro del passeggero.
Il passeggero invece, che ritiene naturale assumere l'automobile come proprio SR, farà il seguente ragionamento:
L'auto è ferma rispetto a me, ma si trova immersa in un campo di forze che mi spinge verso destra, cioè in direzione opposta al centro di rotazione. Si tratta allora di una forza centrifuga, che si manifesta quando l'automobile percorre una curva.
Sono validi entrambi i ragionamenti, ma non si deve dimenticare che la forza centrifuga è fittizia: l'unica forza reale è quella centripeta perché è data dall'adesione del pneumatico sulla strada. In ultima analisi essa si riconduce ad una delle quattro forze fondamentali: quella elettrica.
E’ però evidente che tutti i SR devono essere equivalenti, cioè fornire le stesse predizioni numeriche per forze e accelerazioni. In sostanza, per tutti i SR devo poter applicare la seconda legge di Newton:
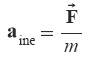 |
(1) |
Il pedice serve ad indicare il sistema di riferimento a cui si riferisce la grandezza: in questo caso stiamo eguagliando l'accelerazione in un sistema di riferimento inerziale al rapporto tra forze agenti e massa del corpo.
Vi sono però particolari SR che si distinguono da tutti gli altri.
Sono quelli in moto accelerato. Se vogliamo che il principio enunciato
sopra sia valido, dobbiamo introdurre in questi sistemi delle forze
fittizie, che nel caso del moto circolare, sono la cosiddetta forza
centrifuga e l'accelerazione complementare, o di Coriolis, dal nome di
colui che enunciò il relativo teorema nel 1835.
Si chiamano fittizie perché non
hanno realtà fisica, emergono solo in particolari sistemi di riferimento. Le
uniche forze degne di tale nome sono le quattro forze fondamentali: quella
gravitazionale, elettrica, nucleare debole e nucleare forte. Nessun effetto fisico può scaturire da una forza fittizia:
esisterà sempre un SR in cui tale forza scompare.
Un'altra differenza tra le forze reali e quelle fittizie si evidenzia alla luce della terza legge di Newton. Le forze reali sono sempre accompagnate da forze di reazione. La terza legge di Newton stabilisce che "se un corpo A esercita una forza sul corpo B, allora B esercita una forza eguale ed opposta sul corpo A". Tuttavia le forze fittizie non sono esercitate da corpi materiali. Esse non hanno "sorgenti", sono semplicemente degli artifici contabili per far tornare i conti nei sistemi di riferimento rotanti.
Ecco perché non possiamo trovare alcuna forza di reazione a forze fittizie e quindi ecco perché non possiamo applicare la terza legge di Newton alle forze fittizie. Non vi è alcun "corpo A" che sta esercitando la forza fittizia.
In sistemi di riferimento non inerziali, la seconda legge della dinamica assumerà quindi una forma diversa. Per un sistema di riferimento in moto rototraslatorio con velocità angolare costante, possiamo scrivere l'accelerazione vista dal riferimento inerziale come:
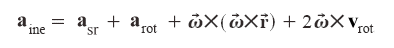 |
(2) |
Cioè l'accelerazione vista dal riferimento inerziale è la somma dell'accelerazione del sistema di riferimento (sr), detta anche accelerazione di trascinamento, della accelerazione manifestata nel sistema di riferimento in rotazione (rot) e di due quantità chiamate, rispettivamente, accelerazione centripeta e di Coriolis.
Quindi se vogliamo che anche nel sistema di riferimento non inerziale valga la seconda legge di Newton, ricordando la (1) e la (2) dovremo scrivere:
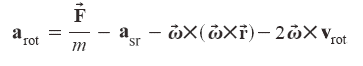 |
(3) |
Nel prosieguo dell'articolo vedremo diversi casi, che tratteremo secondo lo stesso schema:
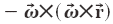 , sempre diretta in direzione opposta al centro della rotazione e quella di Coriolis
, sempre diretta in direzione opposta al centro della rotazione e quella di Coriolis 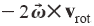 , la cui direzione dipende dalla velocità del punto rispetto al centro del SR.
, la cui direzione dipende dalla velocità del punto rispetto al centro del SR. Forza reale - forze fittizie = m * (accelerazione + Δ)
Un'ultima considerazione va dedicata al classico trabocchetto sui sistemi di riferimento. Il lettore provi a rispondere alla seguente domanda: il seguente sistema di riferimento sta traslando o ruotando? La risposta nel prosieguo dell'articolo.

Fig. 1 - il sistema di riferimento sta ruotando o traslando?
Cominciamo col dire che la spiegazione completa delle maree, che renda conto della loro periodicità e intensità, è estremamente complessa. Qui ci limiteremo a considerare un modello semplificato che vede la Terra sferica, liscia e omogenea, coperta da un velo uniforme d’acqua. Attorno ad essa rivolve una Luna puntiforme in orbita circolare, o meglio, entrambe rivolvono attorno al comune centro di massa. Trascuriamo la presenza del Sole, che qualitativamente non aggiunge nulla al modello.
Dato che la rotazione terrestre non ha effetti sull’esistenza delle due ondate di marea, supporremo che la Terra non stia ruotando su se stessa e che quindi mantenga l’orientamento rispetto alle stelle fisse. Se il lettore avesse delle perplessità su questo punto, lo invitiamo a considerare che la rotazione della terra provoca sì una deformazione della sua figura, ma simmetrica rispetto all'asse. Di conseguenza la Terra si trasformerà da sfera a ellissoide oblato, ma l'equatore manterrà la forma circolare. Quindi la rotazione terrestre non ha effetto sull'esistenza delle maree.
Alcuni dati fisici: nel nostro modello abbiamo un pianeta, la Terra, di massa 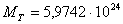 kg ed il
suo satellite, la Luna, di massa
kg ed il
suo satellite, la Luna, di massa 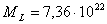 kg.
kg.
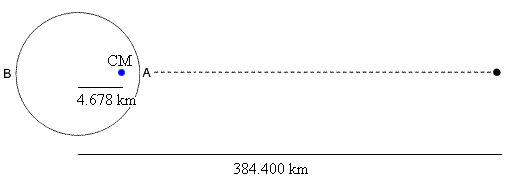
Fig. 2
Il rapporto di massa vale 81,17 la loro distanza R
vale 384.400 km.
Il centro di massa CM dista dal centro della Terra
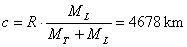 |
(4) |
Dato che il raggio equatoriale terrestre r vale 6378 km, il centro di massa è interno alla Terra, alla profondità di 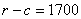 km.
km.
Il centro della Terra descrive dunque un cerchio di raggio c
attorno al CM, anche la Luna descrive un cerchio, ma di raggio 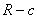 .
.
La velocità angolare di questi moti si ricava dalla terza
legge di Keplero:
|
(5) |
Affrontiamo ora il problema delle maree nel modo più semplice: come se la Terra fosse in caduta libera verso la Luna. Immaginiamo di fotografare la situazione nell’istante in cui la distanza tra i centri è proprio R. Per analizzare la situazione ci mettiamo in un sistema di riferimento solidale col centro della Terra. Dato che si tratta di un sistema di riferimento non inerziale poiché è accelerato dall'attrazione gravitazionale della Luna, dovremo introdurre una accelerazione fittizia uguale ed opposta:
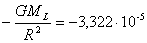 m/s² m/s² |
(6) |
rivolta cioè in direzione opposta alla Luna.
Cinematica
Dal punto di vista cinematico, in questo sistema di riferimento fotografato all'istante in cui la Terra e la Luna si trovano alla distanza R, tutti i punti della superficie terrestre sono fermi, la Luna invece corre incontro alla Terra di moto accelerato.
Dinamica
Calcoliamo l'accelerazione totale di A e B, facendo riferimento all'equazione (3) come la somma di:
- accelerazione gravitazionale lunare
- accelerazione fittizia
Il risultato verrà eguagliato alla accelerazione cinematica del punto,
pensato solidale con la figura terrestre, più una componente, chiamata  , che rappresenta la forza di marea, cioè quella forza che tende a deformare la superficie terrestre.
, che rappresenta la forza di marea, cioè quella forza che tende a deformare la superficie terrestre.
Facendo attenzione al verso dei vettori, per A possiamo scrivere:
|
(7)
|
Mentre per B potremo scrivere:
|
(8)
|
L’ordine di grandezza è 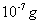 cioè un decimilionesimo
dell’accelerazione di gravità.
cioè un decimilionesimo
dell’accelerazione di gravità.
 |
|
|
Fig. 3 |
Fig. 4 |
Fig. 5 |
| L'accelerazione gravitazionale dovuta alla Luna per tre punti della Terra. | Dopo aver sottratto l'accelerazione fittizia di questo particolare sistema di riferimento, emergono forze che tendono a stirare il pianeta lungo la congiungente Terra-Luna. | Effettuando il calcolo per tutti i punti dell'equatore terrestre, emerge il noto campo di forza mareale. |
Ecco dimostrata l’esistenza di due ondate di marea, in direzioni opposte e lievemente diverse per intensità, essendo maggiore quella rivolta verso la Luna. E’ tutto ciò che serve: l’effetto di marea è dovuto soltanto al gradiente della forza di gravità.
Va sottolineato che l'altezza delle maree non è dovuta allo "stiramento" delle masse d'acqua. Come si vede dalla terza figura, in alcuni punti della superficie la forza di marea è tangente ad essa, ciò implica che le acque sono spinte verso il punto sublunare o quello antilunare, ove si raccolgono.
Il fatto che nella realtà la Terra e la Luna siano in orbita reciproca comporta una accelerazione centripeta o centrifuga (dipende dal sistema di riferimento). E’ però interessante mostrare che essa non ha alcun ruolo nella formazione delle maree, come si vedrà negli esempi seguenti.
In questo secondo esempio e in quelli successivi, supporremo che la Terra e la Luna siano in orbita circolare.
Scegliamo il sistema di riferimento inerziale nel centro di massa del sistema Terra-Luna. Tale punto è fermo rispetto al resto dell’Universo, inoltre il sistema di riferimento non ruota, dunque nella nostra trattazione non compariranno forze fittizie.
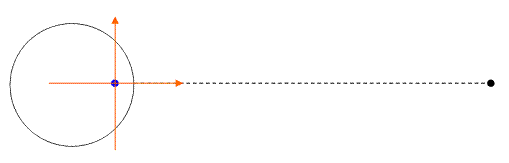
Fig. 6
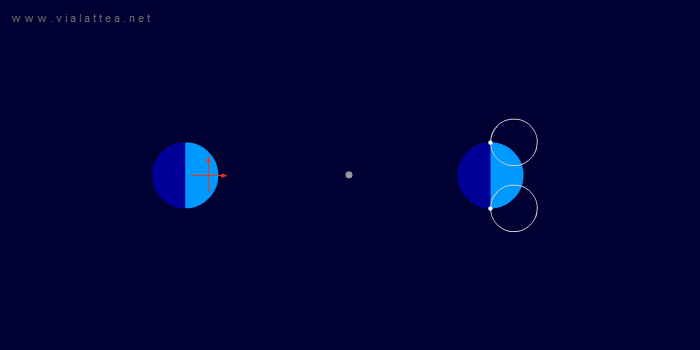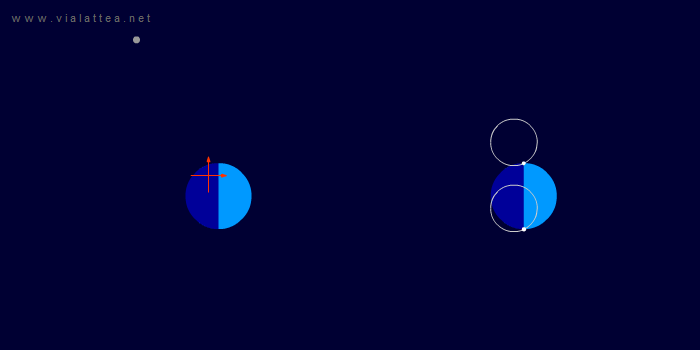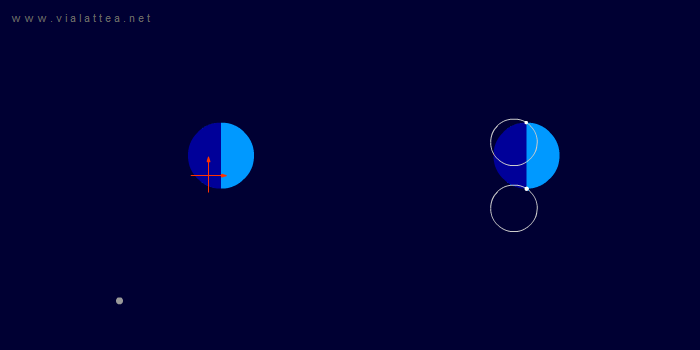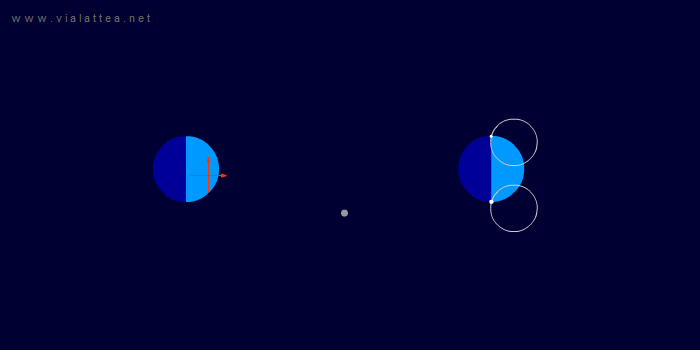
Fig. 7 - A sinistra: la situazione vista da un sistema di riferimento inerziale. Il sistema di riferimento scelto per studiare il problema è anch'esso inerziale ed è marcato con le frecce di colore arancio.
A destra, la dimostrazione visiva che ogni punto della Terra descrive circonferenze uguali, dunque uguali al moto del dentro della Terra attorno al CM.
Cinematica
Il centro della Terra descrive un'orbita circolare di raggio c attorno al CM, con velocità angolare ω.
Per quanto riguarda i punti della superficie terrestre, occorre evitare un fraintendimento, peraltro molto comune.
Dire che il centro della Terra ruota attorno al CM non significa che tutta la Terra stia ruotando attorno a tale punto! La Terra infatti, per come abbiamo schematizzato la situazione, è ferma rispetto alle stelle fisse. Non ruota su se stessa, sta traslando. Ecco dunque la risposta al quesito di figura 1. Tutti i suoi punti descrivono cerchi di eguale raggio c ma di centro diverso.
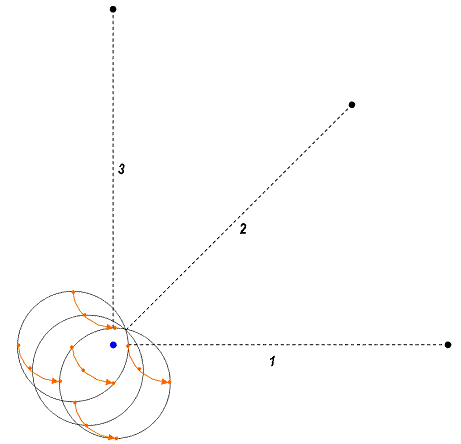
Fig. 8
Essa si muove attorno al centro di massa mantenendo la sua figura parallela a se stessa. Non esiste pertanto alcuna forza fittizia (centrifuga) associata alla presunta rotazione della Terra attorno a CM.
E’ sbagliato allora il seguente calcolo. Alcuni autori vogliono
calcolare l’effetto della forza centrifuga operando come segue: se è
vero che la Terra ruota attorno al CM, allora l’accelerazione
centrifuga in A vale 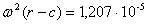 m/s² mentre in B vale
m/s² mentre in B vale 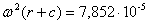 m/s².
m/s².
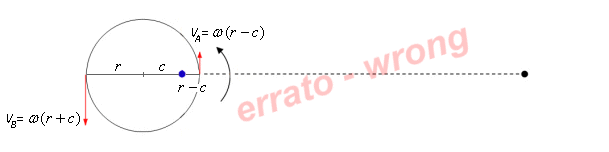
Fig. 9
Si ottiene l’assurdo che l’intensità della accelerazione centrifuga in B vale circa 6,5 volte quella in A. Probabilmente è questo fatto a trarre in inganno coloro i quali affermano che la marea opposta alla Luna è provocata dalla forza centrifuga!
D’altra parte, questo calcolo porta ad una accelerazione che è più di 70 volte quella di marea, quindi c’è davvero qualcosa di sbagliato.
E' invece corretto affermare che tutti i punti della Terra descrivono un cerchio di raggio c e subiscono quindi una accelerazione di intensità 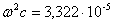 m/s² diretta verso il centro del cerchio.
m/s² diretta verso il centro del cerchio.
Dinamica
Dato che il SR scelto è inerziale, non compaiono forze fittizie, l'unica forza sarà quella - reale - dovuta all'attrazione gravitazionale.Per il punto A possiamo scrivere:
|
(9)
|
La forza di marea quindi è rivolta in direzione della Luna, come nel caso precedente.
Per il punto B possiamo scrivere:
|
(10)
|
In questo caso la forza di marea è rivolta in direzione opposta alla Luna.
Torniamo a 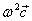 e rielaboriamo questa quantità, tenendo
conto della definizione di c e di
e rielaboriamo questa quantità, tenendo
conto della definizione di c e di 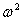 viste nelle equazioni (4) e (5).
viste nelle equazioni (4) e (5).
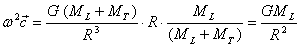 |
(11) |
Cioè il campo uniforme di accelerazioni centripete ha la stessa intensità dell’attrazione lunare al centro della Terra! Naturalmente questa non è una coincidenza, è l’espressione matematica del fatto che il centro della Terra è in orbita, attratto dalla Luna.
Abbiamo quindi ottenuto gli stessi risultati anche se la Terra e la Luna orbitano l’una attorno all’altra.
Scegliamo il sistema di riferimento ancora nel centro di
massa, ma stavolta in rotazione con velocità angolare pari al sistema
Terra-Luna, che pertanto appariranno fisse. Di conseguenza nella nostra
trattazione dovremo introdurre per ogni punto della Terra due accelerazioni fittizie: quella centrifuga e quella di Coriolis. La prima ha origine in CM e intensità 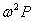 dove P è la distanza del punto dal
CM.
dove P è la distanza del punto dal
CM.
La seconda ha intensità
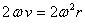 ed il verso è dato dal prodotto vettoriale tra ω e v, cambiato di segno.
ed il verso è dato dal prodotto vettoriale tra ω e v, cambiato di segno.

Fig. 10
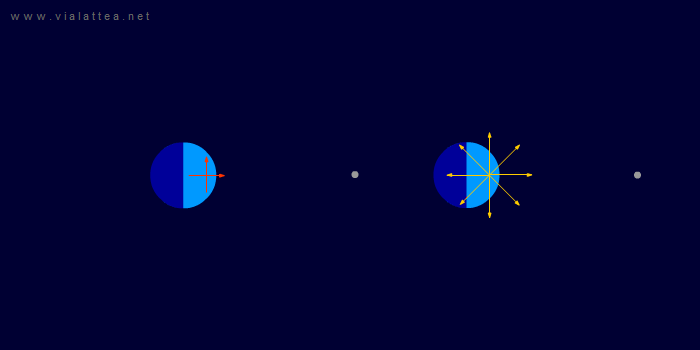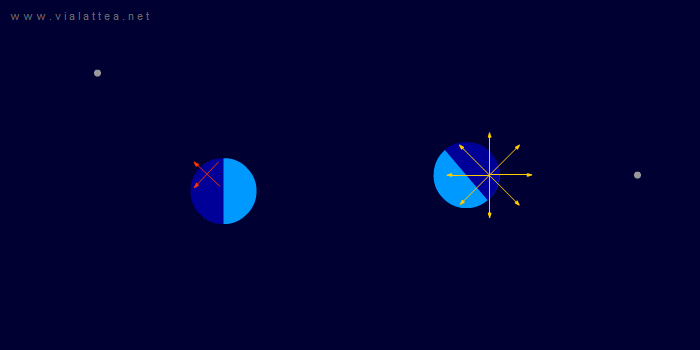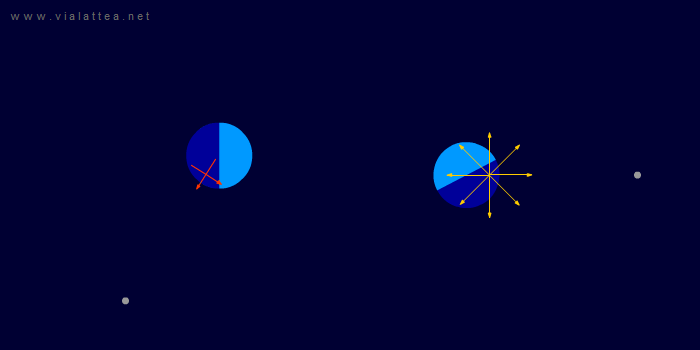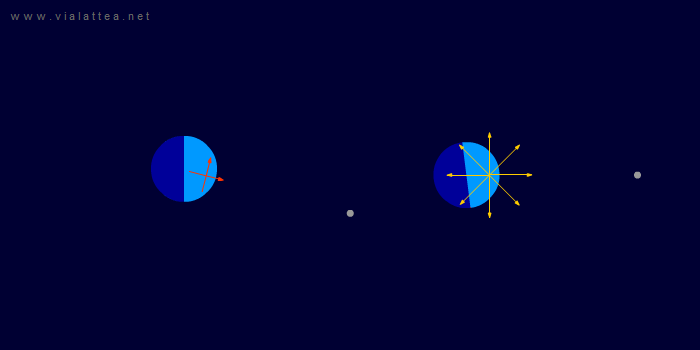
Fig. 11 - A sinistra: la situazione vista da un sistema di riferimento inerziale. Questa volta il sistema di riferimento che andremo a scegliere ruota in modo da mantenere ferme la Terra e la Luna.
A destra: è evidente che in questo sistema di riferimento la Terra esibisce una rotazione sul proprio asse. Inoltre, sorge un campo di forze centrifughe con centro in CM. Nella rappresentazione manca il campo di forze di Coriolis.
Possiamo esprimere questo campo di accelerazioni centrifughe in un modo più semplice: come la somma di un campo radiale, con origine nel centro della Terra, e un campo di accelerazioni uguali e parallele.
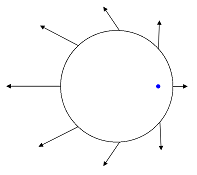 |
= | 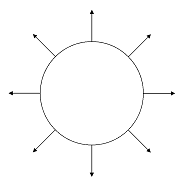 |
+ | 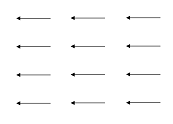 |
| Fig. 12 | ||||
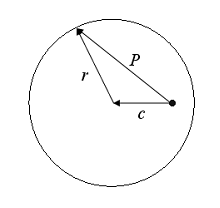 |
Fig. 13 |
Infatti il vettore P può essere scomposto in due vettori: 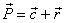 .
.
E dunque anche 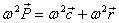 .
.
Notiamo che 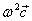 è una grandezza costante: non dipende dal
punto P considerato, mentre la grandezza
è una grandezza costante: non dipende dal
punto P considerato, mentre la grandezza 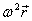 è una accelerazione radiale isotropa.
è una accelerazione radiale isotropa.
Alcuni autori si sono fatti ingannare da quest’ultimo campo, attribuendogli un significato fisico reale. Spesso gli si attribuisce la facoltà di contribuire al rigonfiamento equatoriale. In realtà non è possibile che esista tale forza, per giunta soltanto in questo sistema di riferimento!
Questo campo radiale viene compensato dalle forze di Coriolis, come si leggerà di seguito.
Occorre prestare molta attenzione al seguente fatto: se il sistema di riferimento è in rotazione ma la Terra è fissa rispetto al resto dell’Universo, essa in tale rappresentazione apparirà in rotazione con una velocità angolare opposta! (vedi animazione)
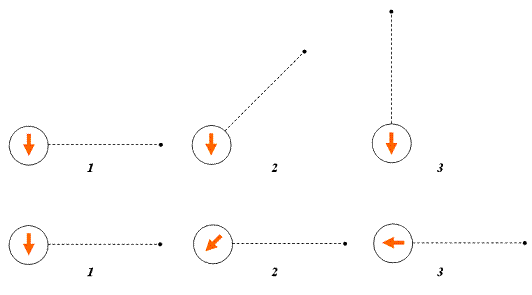
Fig. 14
Cinematica
Il centro della Terra è fermo, invece tutti i punti della
superficie terrestre, in particolare i nostri A e B, ruotano in senso orario e
quindi esibiscono una accelerazione di intensità 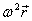 diretta verso il centro della Terra.
diretta verso il centro della Terra.
Dinamica
Calcoliamo le accelerazioni dei punti A e B, come somma di:
- accelerazione gravitazionale lunare
- componente uniforme dell’accelerazione centrifuga
- componente radiale dell’accelerazione centrifuga
- accelerazione di Coriolis.
Facendo attenzione al verso dei vettori, per il punto A possiamo scrivere:
|
(12) |
ma tutti i termini in
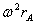 si cancellano, dunque
si cancellano, dunque
|
Per il punto B sarà, ricordando che i vettori 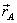 e
e 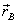 sono opposti,
sono opposti,
|
(13) |
anche stavolta tutti i termini in
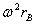 si cancellano, dunque
si cancellano, dunque
|
La cancellazione dei termini in ω²r non deve meravigliare: un po’ di immaginazione fa capire che la rotazione dovuta al sistema di riferimento viene esattamente compensata dalla controrotazione. Tutta questa confusione deriva dalla scelta del sistema di riferimento: nel nostro modello fisico la Terra se ne sta pacificamente ferma rispetto alle stelle fisse.
Noi invece la vogliamo descrivere in un sistema di riferimento rotante: è chiaro che essa dovrà esibire una controrotazione.
Il campo radiale dunque viene cancellato. Rimane il solo campo uniforme, proprio come nel secondo caso.
Il centro della Terra è sottoposto al campo uniforme di accelerazioni 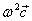 e all’accelerazione di gravità lunare
che, come abbiamo visto, hanno valore identico. La somma è zero, infatti il centro
della Terra è fermo. Il che è perfettamente ragionevole: le forze fittizie
servono proprio per poter applicare la consueta legge F=ma.
Pertanto, se nel sistema di riferimento il centro della Terra appare fermo, è
perché l’attrazione gravitazionale della Luna e la forza fittizia sono
identiche.
e all’accelerazione di gravità lunare
che, come abbiamo visto, hanno valore identico. La somma è zero, infatti il centro
della Terra è fermo. Il che è perfettamente ragionevole: le forze fittizie
servono proprio per poter applicare la consueta legge F=ma.
Pertanto, se nel sistema di riferimento il centro della Terra appare fermo, è
perché l’attrazione gravitazionale della Luna e la forza fittizia sono
identiche.
Di nuovo, i valori numerici tornano, nonostante il sistema di riferimento abbia introdotto delle complicazioni.
Il lettore sarà rimasto di certo perplesso a proposito della rotazione della Terra. Ci preme ribadire che anche se introducessimo una rotazione terrestre nel modello fisico, l’effetto sarebbe di aumentare il diametro equatoriale della Terra, facendola diventare un ellissoide oblato. Tale deformazione però è simmetrica e non produce le maree.
Scegliamo il sistema di riferimento nel centro della Terra e solidale rispetto alle stelle fisse. E’ quello più usato per rappresentare il campo vettoriale delle forze di marea. L’unico inconveniente è che tale campo vettoriale sarà in rotazione, ma per i nostri scopi basterà immaginarlo congelato ad un istante.
Dobbiamo ricordare quello visto nel caso 2: la Terra non sta
ruotando, bensì traslando secondo un percorso circolare! Di conseguenza
nella nostra trattazione dovremo introdurre soltanto una accelerazione
fittizia uniforme, rivolta in direzione opposta alla Luna, con
intensità 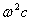 . Essa è dovuta al fatto che il centro del sistema di riferimento sta ruotando attorno a CM.
. Essa è dovuta al fatto che il centro del sistema di riferimento sta ruotando attorno a CM.
Gli assi del sistema di riferimento infatti non variano l'orientazione rispetto alle stelle fisse: questo sistema di riferimento - come quello di figura 1 - sta traslando.
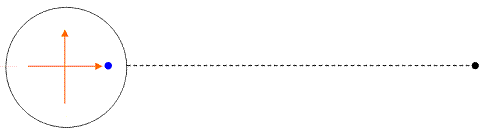
Fig. 15

Fig. 16 - A sinistra, la situazione vista da un sistema di riferimento inerziale. In questo quarto caso il sistema scelto è solidale col centro della Terra. La situazione è dunque analoga al secondo caso.
A destra, infatti, è evidenziato il campo uniforme di forze centrifughe.
Cinematica
Il CM ruota attorno al centro della Terra con velocità angolare ω. Tutti i punti della Terra invece sono fermi.
Dinamica
Calcoliamo le accelerazioni dei punti A e B, come somma di:
- accelerazione gravitazionale lunare
- accelerazione fittizia.
Facendo attenzione al verso dei vettori: l’accelerazione di A sarà
|
(14)
|
Mentre quella di B sarà:
|
(15)
|
Di nuovo, il risultato è identico al caso 2, qui però è forse più facile accettare l’esistenza di un campo uniforme di accelerazioni fittizie perché viene “trasferito” al sistema di riferimento.
L’attrazione gravitazionale della Luna sul centro della Terra è esattamente pari all’accelerazione centrifuga: non esistendo forze nette, la Terra appare ferma.
Scegliamo il sistema di riferimento nel centro della Luna e rotante assieme alla Terra. Apparentemente si tratta di una scelta bizzarra, di nessun interesse pratico, invece mostra un punto di vista nel quale sorgono più forze fittizie, ma ancora una volta – sorprendentemente – si compensano e lasciano il “solito” risultato finale.
Cinematica
La Terra e la Luna sono ferme, ma la Terra ruota sul proprio asse in senso orario con velocità angolare ω.
Tutti i punti della superficie terrestre dunque hanno una accelerazione centripeta di modulo 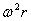 .
.
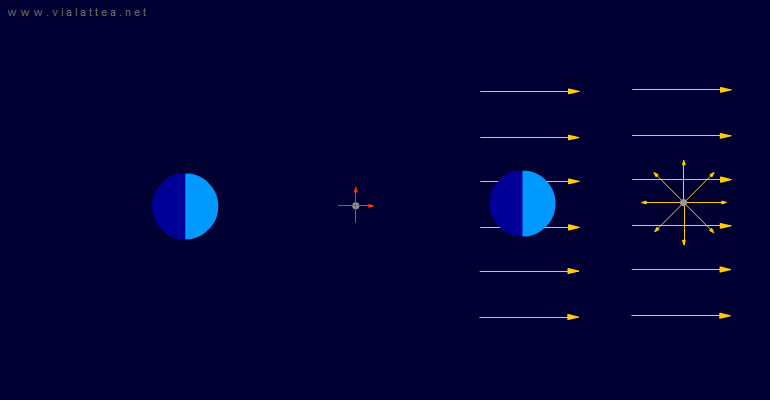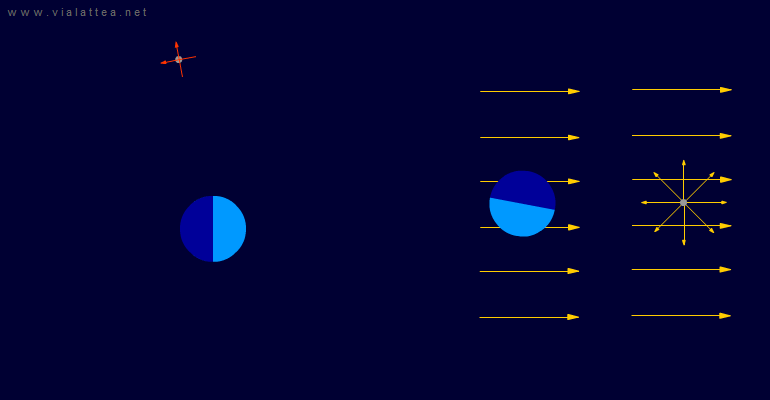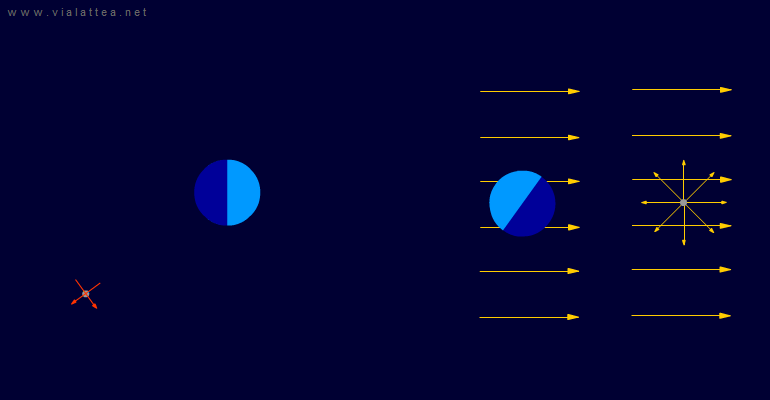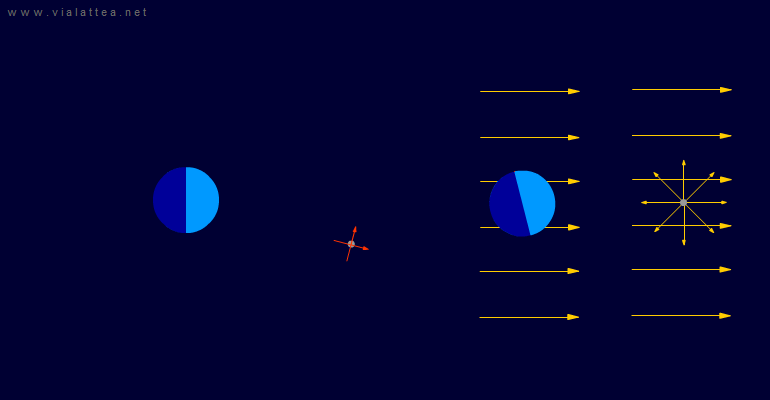
Fig. 17 - A sinistra, la situazione vista da un sistema di riferimento inerziale. In questo quinto caso il sistema scelto è solidale col centro della Luna e rototraslante.
A destra sono evidenziati i due campi di forze apparenti: uno uniforme e l'altro radiale centrato sulla Luna. Nella rappresentazione manca il campo di forze di Coriolis.
Dinamica
Questo sistema di riferimento non solo ruota su se stesso, ma compie un percorso circolare attorno al CM. Pertanto è in moto rototraslatorio, che genera ben tre campi di forze apparenti.
Uno è uniforme, con accelerazione di intensità 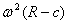 ed è dovuto alla traslazione del centro del sistema di riferimento attorno al CM.
ed è dovuto alla traslazione del centro del sistema di riferimento attorno al CM.
Gli altri due sono dovuti alla rotazione del SR attorno alla propria
origine. Essa genera una accelerazione centrifuga di intensità 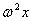 dove con x abbiamo indicato la distanza dalla Luna dal punto di cui vogliamo
calcolare l'accelerazione. Genera poi una accelerazione di Coriolis la
quale - come già detto - ha intensità
dove con x abbiamo indicato la distanza dalla Luna dal punto di cui vogliamo
calcolare l'accelerazione. Genera poi una accelerazione di Coriolis la
quale - come già detto - ha intensità 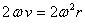 ed il verso è dato dal prodotto vettoriale tra ω e v, cambiato di segno.
ed il verso è dato dal prodotto vettoriale tra ω e v, cambiato di segno.
Ripetiamo il calcolo delle accelerazioni per i punti A e B, come somma di:
- accelerazione gravitazionale lunare
- accelerazione fittizia uniforme
- accelerazione fittizia centrifuga
- accelerazione fittizia di Coriolis .
Facendo attenzione al verso dei vettori: l’accelerazione di A sarà
|
(16) |
ma tutti i termini in 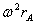 e ω²R si cancellano, dunque
e ω²R si cancellano, dunque
|
Mentre quella di B sarà, ricordando che i vettori 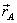 e
e 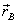 sono opposti,
sono opposti,
|
(17) |
anche stavolta tutti i termini in 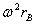 e ω²R si cancellano, dunque
e ω²R si cancellano, dunque
|
Di nuovo, abbiamo ottenuto lo stesso risultato dei due casi precedenti.
Fermiamoci a riflettere su un fatto importante, emerso nelle diverse trattazioni.
Alla attrazione lunare nei diversi punti della superficie terrestre si deve sottrarre sempre un campo uniforme, il cui valore guarda caso è esattamente pari all’attrazione lunare al centro della Terra. Perché?
La risposta sta nel significato profondo della condizione “essere
in orbita attorno ad un corpo celeste”. Questa condizione è equivalente, sotto
tutti i punti di vista, all’essere in caduta libera.
La Terra è in caduta libera verso la Luna, attratta dalla forza gravitazionale. Per questo motivo essa subisce una accelerazione
uniforme di intensità 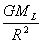 Dato che però non cade in moto
rettilineo ma è in orbita, tale accelerazione lineare si “trasforma” in una
accelerazione centripeta
Dato che però non cade in moto
rettilineo ma è in orbita, tale accelerazione lineare si “trasforma” in una
accelerazione centripeta 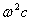 , di pari intensità.
, di pari intensità.
Il fatto che la Terra ruoti attorno al CM o su se stessa purtroppo getta fumo negli occhi: questi effetti non introducono alcuna deformazione mareale, in compenso hanno buon gioco a confondere le idee.
Desidero ringraziare Donald E. Simanek, il cui articolo ha ispirato il presente lavoro, Mino Saccone, Dieter Kreuer, Salvatore Ganci e Giampiero Barbieri per le proficue discussioni e Andrea del Monte per i suggerimenti sulle animazioni Flash.