Vediamo ora come si calcola l’intensità delle forze di marea :

Schema concettuale : ci poniamo in un campo di forza Newtoniano generato da una sola massa M, e consideriamo trascurabile la massa m del corpo di prova. Calcoliamo la differenza tra la forza gravitazionale che agisce sui piedi dell’omino e la forza che agisce sulla testa dell’omino.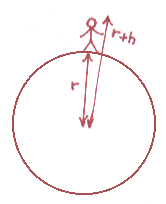

Ricaviamo la formula :

L’espressione della forza di gravità secondo Newton è la seguente :

dunque la forza differenziale tra la testa ed i piedi dell’omino è data da :

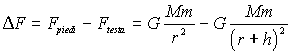
raccogliamo a fattore comune

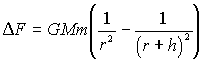
sviluppando l’espressione tra parentesi otteniamo :

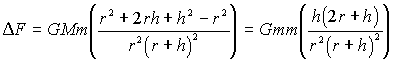
questa è la formula finale esatta.

Seguono alcune considerazioni sulla bontà dell'approssimazione che abbiamo introdotto. I grafici seguenti sono riferiti alla situazione di un omino alto 2m in piedi sulla superficie terrestre.

Quando le variabili che compaiono in una espressione hanno ordini di grandezza molto diversi, è possibile effettuare qualche semplificazione.

Nel nostro caso possiamo senz’altro affermare che r è molto maggiore di h, perché l’altezza dell’omino è fissata a 2 metri, mentre il raggio terrestre è di 6.370.000 metri.

Dunque 2r+h lo possiamo approssimare a 2r. Idem per il denominatore, dove r+h lo approssimiamo a r. L’espressione semplificata è :

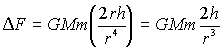
Abbiamo ottenuto una formula molto comoda, che ci permette con poca fatica di calcolare la forza di marea.

Potrebbero sorgere dei dubbi legittimi relativi alla nostra approssimazione : quanto è buona l’approssimazione ? Quando diventa inaccettabile ?

Una risposta rigorosa richiede l’analisi della propagazione degli errori, cioè studiare come le incertezze relative ad un dato si trasmettono, amplificate, quando si effettuano dei calcoli.

A noi basta l’aiuto di un calcolatore, dove un comunissimo programma ci permette di disegnare il grafico di due funzioni : quella esatta (tracciata in blu) e quella approssimata (tracciata in rosso) come si vede, esse coincidono, a tal punto che la funzione esatta è sovrascritta da quella approssimata.

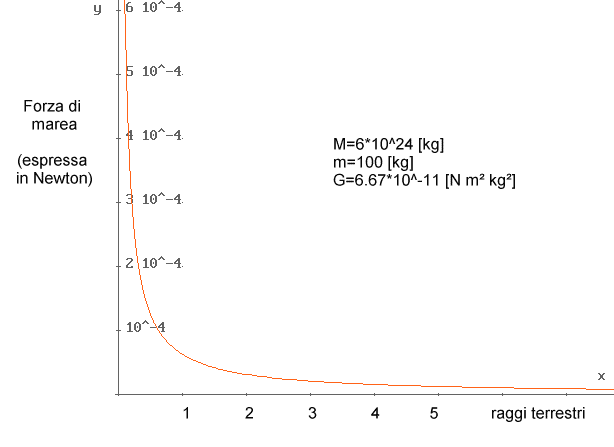
Questo grafico però non ci aiuta molto : siamo già nella condizione ottimale in cui h è molto minore di r.

Ora rimuoviamo l’ipotesi che h << r e poniamoci la domanda : quanto sbaglia la funzione approssimata quando aumenta il rapporto fra h / r ?

Schema concettuale : vogliamo un’espressione che, noto il rapporto h/r, ci dia una misura di quanto peggiora la stima utilizzando la funzione approssimata. Come indice di quanto peggiora la stima pensiamo allo scarto tra le due funzioni rispetto a quella esatta. Questo indice è chiamato errore relativo ; moltiplicando l’errore relativo per 100 si ottiene l’errore percentuale.

Ricaviamo la formula:

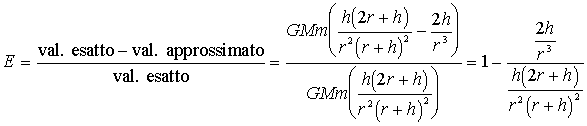
se fissiamo r=1 automaticamente h assumerà il significato di rapporto h/r e, con qualche passaggio, otteniamo alla fine l’espressione cercata :

tracciamo il grafico di questa funzione :

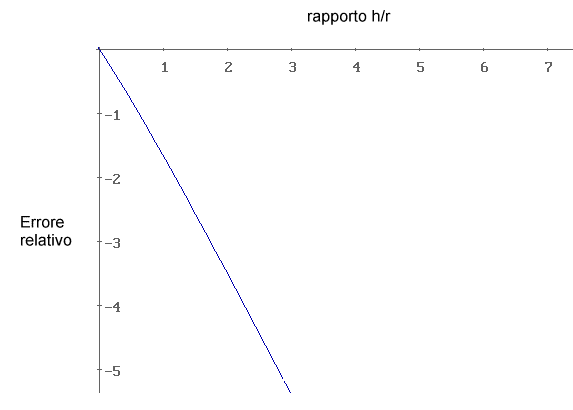
Vediamo che per h =0 l’errore relativo vale 0, questo significa che per h molto piccoli rispetto a r non abbiamo errore. Il fatto che la funzione sia negativa significa che la formula approssimata dà un valore più elevato di quella esatta: infatti se

allora

val. approssimato > val. esatto

Per h crescente l’errore aumenta più che linearmente. Ad esempio, per h =2 otteniamo E= - 3.5, cioè quando la distanza tra la testa e i piedi dell’omino raggiunge il valore di 2 raggi terrestri, il valore della forza di marea calcolato con la formula approssimata è in eccesso del 350% rispetto al valore corretto.