La velocità di fase di un’onda elettromagnetica è la velocità con cui si propaga il fronte a fase costante. Nel vuoto, o in un mezzo non dispersivo, le onde a tutte le frequenze hanno la stessa velocità (c), quindi anche la velocità di gruppo e la velocità del segnale hanno quel valore. L’unica velocità che ha veramente significato fisico è la velocità del segnale, cioè la velocità di trasferimento dell’informazione. Un segnale più veloce della luce (nel vuoto) creerebbe problemi di causalità: il segnale potrebbe arrivare al destinatario prima di essere stato inviato, e quindi essere utilizzato per creare un effetto prima della causa.
Un’onda monocromatica in senso matematico non esiste, perché dovrebbe estendersi per un tempo infinito. Non avrebbe nemmeno utilità come segnale perché l’informazione trasportata è nulla. La velocità di fase di un’onda monocromatica inoltre non può essere misurata. Un pacchetto d’onda, cioè un impulso con una frequenza centrale, una banda e una durata limitata, invece, rappresenta un tipico segnale realistico. Nel vuoto, o nei mezzi non dispersivi, le varie componenti (cioè le onde monocromatiche che lo compongono) viaggiano tutte alla stessa velocità e quindi la forma dell’impulso non cambia e come detto la velocità di gruppo è uguale alla velocità di fase e coincide in questo caso con la velocità dell’informazione.
I mezzi come il vetro o l’acqua sono invece dispersivi, cioè la velocità varia a seconda della frequenza, e quindi la forma di un impulso cambia. Usualmente le alte frequenze vengono ritardate e l’impulso si allarga, (da cui il termine dispersione). Tuttavia ci possono essere delle frequenze in cui il comportamento è anomalo, ad esempio vicino ai picchi di assorbimento (risonanze), in cui le frequenze più alte vengono ritardate meno di quelle più basse (dispersione anomala). In questo caso l’impulso viene compresso e il fronte di salita avanza facendo sì che l’inviluppo dell’impulso (velocità di gruppo) vada ad una velocità superiore a quella della luce nel vuoto. Le onde componenti viaggiano quindi sempre a velocità minori o uguali a quella della luce nel vuoto. Anche la velocità dell’informazione è sempre inferiore o uguale a quella della luce nel vuoto, anche se questi fenomeni fanno discutere gli esperti della comunità scientifica.
L’esperimento di Dogariu, Wang e Kuzmich in particolare, sfrutta l’amplificazione dell’impulso di luce (GAS: Gain Assisted Superluminal propagation) ottenuta in una cella ai vapori di cesio mantenuto in uno stato eccitato con particolari caratteristiche (1) attraverso un fascio laser. Il principio di quello che avviene nella cella (trasparente) è illustrato chiaramente in questa animazione del Prof. Dogariu, presa dalla sua pagina web
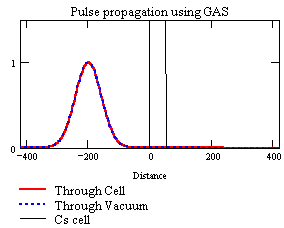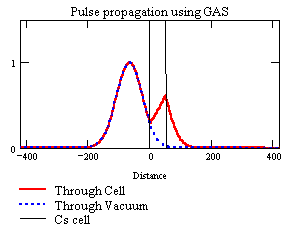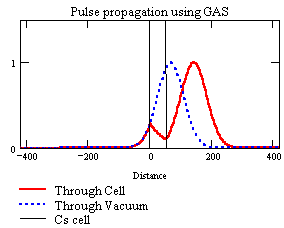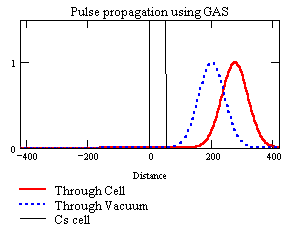
Si vede che l’impulso viaggia sempre alla velocità della luce, ma viene deformato in modo che la parte principale avanzi rispetto alle code.
Anche al CNR è stato condotto un esperimento simile, alle frequenze delle microonde; il comunicato stampa si trova a questo link.
1. il set up dell’esperimento è molto complicato e sono stati utilizzati dei particolari accorgimenti, come la presenza di due picchi di guadagno vicini, che consentono all’impulso di non essere deformato, e la velocità di gruppo negativa (cioè l’impulso viaggia all’indietro) che permette valori più elevati.
Tutto ciò è spiegato negli articoli
- L. J. Wang, A. Kuzmich, and A. Dogariu, “Gain-assisted superluminal light propagation,” Nature 406, (2000)
- A. Dogariu, A. Kuzmich, and L. J. Wang, "Transparent Anomalous Dispersion and Superluminal Light Pulse Propagation at a Negative Group Velocity," Phys. Rev. A (Atomic, Molecular and Optical Physics), (2001).
di cui si trovano facilmente i preprint sul web.