Il teorema del campionamento (di Nyquist-Shannon) afferma che è possibile ricostruire un segnale campionato se questo è limitato in una banda B e se la frequenza di campionamento è maggiore (o uguale) a 2B. (*)
Il segnale telefonico di tipo voce si estende nella banda 300-3400 Hz e viene campionato a 8 kHz soddisfacendo così alla condizione di Nyquist con un certo margine perché i filtri per la ricostruzione non possono avere una transizione netta tra banda passante e banda bloccante.
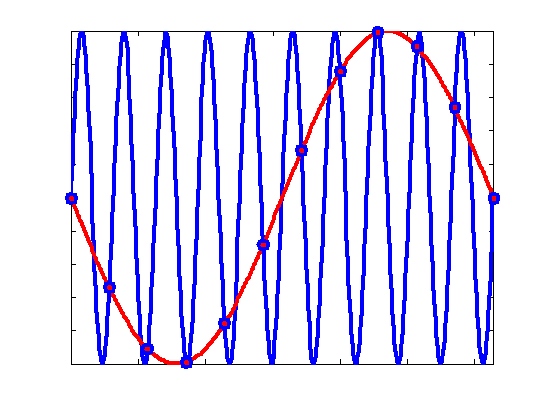
Intuitivamente è comprensibile che se un segnale ha frequenze minori di un certo limite la sua possibilità di variare da un istante ad un tempo successivo sia limitata e proporzionale proprio a questa massima frequenza.
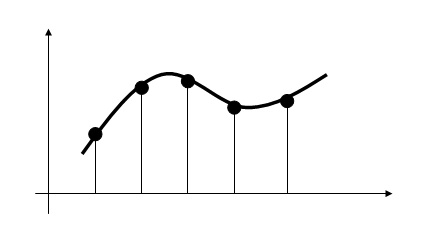
Il fatto di poterlo campionare senza perdere informazione è legato proprio all’ipotesi che tra un campione e l’altro il segnale abbia un comportamento prevedibile in modo da poterlo ricostruire come se dovessimo unire i puntini:
come qui
non come qui
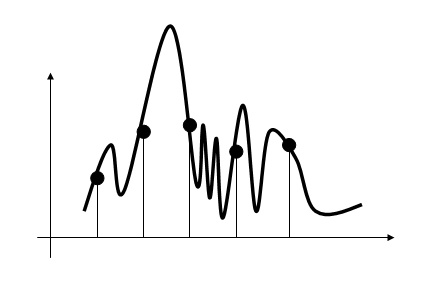
Diamo ora una dimostrazione un po’ più convincente.
Campionare un segnale significa moltiplicarlo per un treno di impulsi c(t).
Nel dominio della frequenza questo equivale a eseguire una convoluzione tra lo spettro del segnale originale e lo spettro del treno di impulsi.
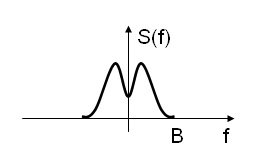
Sia lo spettro del segnale limitato in banda B
lo spettro C(f) del treno di impulsi a passo T è ancora un pettine di impulsi in frequenza a intervalli 1/T.
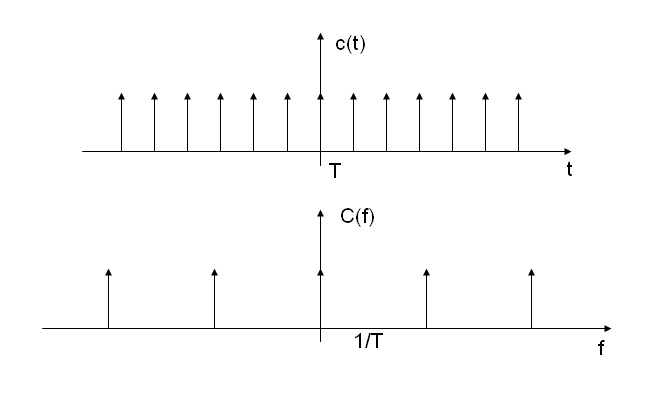
La convoluzione è una successione di repliche dello spettro del segnale originale a passo 1/T; se questo intervallo 1/T è maggiore di 2B le repliche dello spettro non si sovrappongono ed è possibile con un filtro passabasso isolare lo spettro del segnale originale.
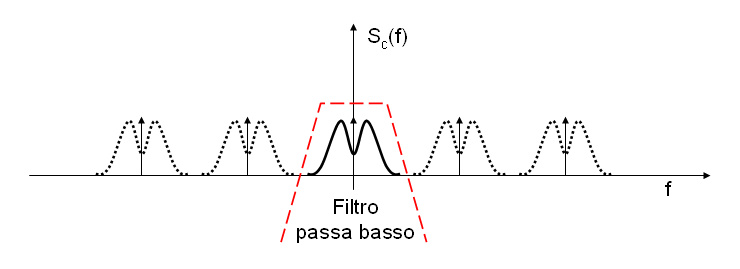
Nel dominio del tempo il filtraggio equivale ad una convoluzione del treno di impulsi corrispondenti ai campioni con la risposta impulsiva del filtro che per un filtro ideale è
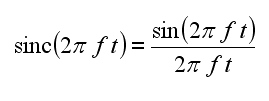
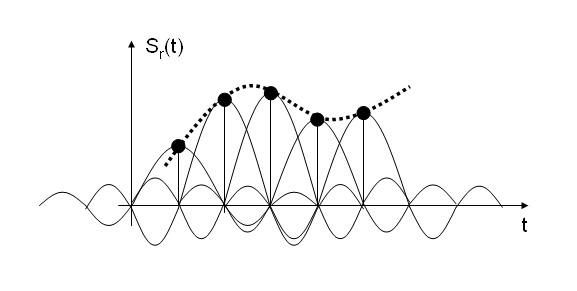
la funzione sinc ha la proprietà di annullarsi per i multipli di T, quindi in corrispondenza di un campione la ricostruzione è garantita da un unica sinc, mentre tra un campione e l’altro la somma di tutti i sinc ricalca l’andamento del segnale originale.
Aliasing
Che succcede se invece il tempo di campionamento è superiore a 1/2B? Una parte dello spettro delle repliche si ripiega su quello della banda base, dando luogo ad un disturbo chiamato aliasing.
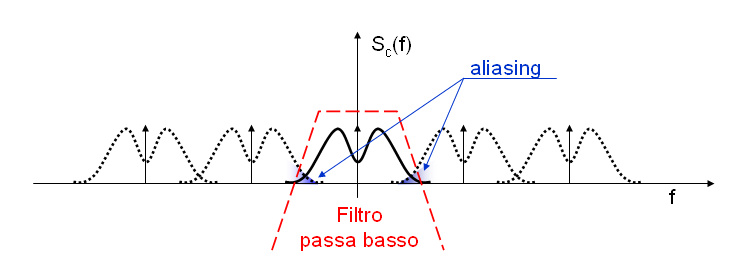
Praticamente una frequenza troppo alta rispetto a quella di campionamento viene interpretata come un segnale a frequenza più bassa
Dominio dello spazio e campionamento bidimensionale
Le stesse considerazioni fatte per segnali nel tempo possono essere estese a segnali nello spazio (ad esempio immagini);
in questo caso la frequenza assume il significato di risoluzione spaziale. L’aliasing è visibile quando si ridimensiona sul computer un’immagine con una trama (come quelle stampate sui giornali)
Qui riporto una foto della testa del cavallo del carro di Selene del frontone del Partenone (si trova al British Museum) elaborata con effetto a stampa a grandezza naturale e ridimensionata; nel ridimensionamento si crea aliasing tra la ripetitività della trama di stampa e il ricampionamento, generando le macchie colorate.


Un altro esempio di aliasing è visibile nella televisione quando compaiono persone con indumenti a righe sottili: se lo spazio tra le righe è inferiore alla risoluzione del segnale televisivo si possono vedere bande colorate analoghe a quelle dell’immagine del cavallo del Partenone.
Il mio professore di Teoria dei Segnali, il bravissimo e simpatico Alessandro Neri, per scherzare sul campionamento e sull’aliasing a lezione freddò la platea con la battuta:
"Se due cercerati vedono uno un cavallo bianco e uno un cavallo nero allora è una zebra"
(*)
Un’estensione ai segnali limitati in banda traslata (cioè da f a f+B, come i segnali modulati) è data dal teorema del campionamento generalizzato (Papoulis, 1977).