Innanzi tutto leggete la esauriente risposta di G.Verbana su Vialattea riguardo la correlazione [1].
Per la definizione e vari esempi di funzioni di autocorrelazione vedete anche l’applet in [2].
Il concetto fondamentale, peraltro già sottolineato da G.Verbana in [1] è che un segnale può essere rappresentato in modo equivalente nel dominio del tempo e nel dominio della frequenza.
Alla forma d’onda corrisponde la trasformata di Fourier (vedete anche [3]), mentre alla autocorrelazione corrisponde la densità spettrale di Energia o di Potenza; in alcuni casi è comodo lavorare nel dominio del tempo, in altri nel dominio della frequenza.
Facciamo un paio di esempi di casi in cui è comodo l’utilizzo della funzione di autocorrelazione.
Il primo esempio riguarda la rivelazione del segnale radar. Il radar (RAdio Detection And Ranging) è un sistema di misura della distanza di oggetti (Target) che utilizza il tempo impiegato da un impulso di radioonde (trasmesso attraverso l’antenna), a raggiungere l’oggetto e – riflettendosi sulla sua superficie – a ritornare indietro fino all’antenna. Il Radar quindi trasmette per un piccolo intervallo di tempo, e poi rimane in ascolto in attesa di eventuali impulsi riflessi.
L’impulso che ritorna, dopo:
• l’attenuazione geometrica del tragitto di andata,
• l’attenuazione dovuta al fatto che solo una piccola parte dell’energia incidente sul target viene riflessa esattamente nella direzione del radar,
• e l’attenuazione geometrica del tragitto di ritorno
(equazione del radar), è molto più basso dell’impulso trasmesso, ed è di solito necessario fare delle operazioni di filtraggio per ridurre il rumore.
Si dimostra nei testi specialistici (vedi ad es. [4, 5]) che il filtro ottimo, nel senso che massimizza il rapporto Segnale / Rumore (il cosiddetto Filtro Adattato o Matched Filter), è un filtro che implementa la correlazione tra l’impulso trasmesso e l’impulso ricevuto.
Come si vede in [2] l’autocorrelazione di un impulso rettangolare è una funzione a triangolo, e il modo migliore per rivelare l’eco radar è porre una soglia in modo opportuno su questa funzione. 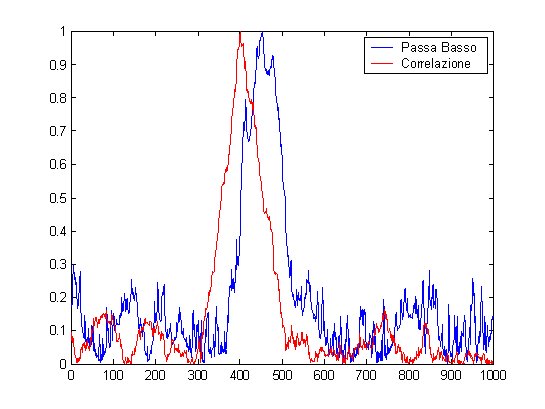
Figura 1 – Confronto tra filtraggio con la correlazione e con un passa basso
Naturalmente, e anche questo è accennato in [1], nulla vieta di poter operare il filtraggio del rumore nel dominio della frequenza, e anzi spesso nei Radar si usa una versione approssimata del Matched Filter, proprio utilizzando un filtro Passa Basso. In Figura 1 sono riportati due esempi di segnali radar, uno filtrato con il filtro a correlazione, e l’altro con un filtro passa basso: si noti che
a) come dice la teoria con il filtro a correlazione il rumore residuo è più basso
b) con la correlazione il picco è molto più preciso, e questo si ripercuote su una migliore accuratezza della misura (il picco della correlazione corrisponde all’istante di inizio dell’impulso filtrato con il passa basso)
ma comunque la rivelazione del segnale è chiara in tutti e due i casi.
Un caso in cui invece è indispensabile utilizzare la correlazione è quando l’impulso è modulato in frequenza; ad esempio con il cosiddetto Chirp (vedi figura 2). Questa tecnica, copiata pari pari da Madre Natura che ne ha fatto dono ai pipistrelli per l’elaborazione del loro segnale Sonar, sfrutta il fatto che la autocorrelazione di impulsi con frequenza linearmente crescente (o decrescente) presenta un picco molto pronunciato (vedi figura 3), molto di più del triangolo che si ha con impulsi rettangolari non modulati, e facilmente individuabile in mezzo al rumore e ai disturbi.
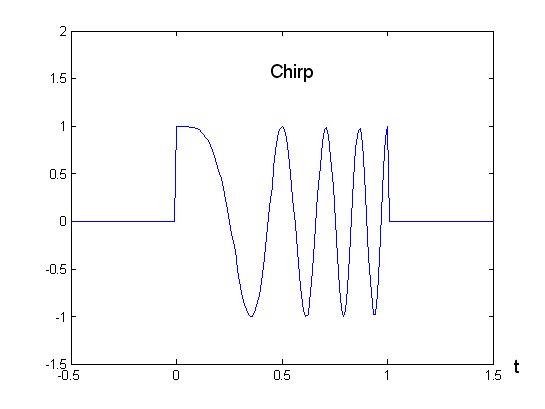
Figura 2 – Andamento temporale del segnale Chirp
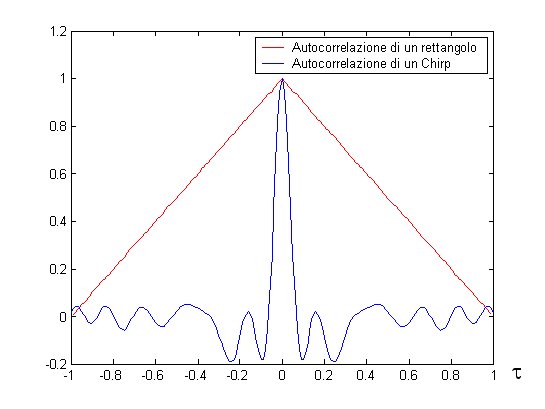
Figura 3 – Autocorrelazione del Chirp e autocorrelazione di un impulso rettangolare
Questa tecnica, inizialmente sviluppata nell’ambito dei radar, si sta via via espandendo ad altri campi, come quello delle comunicazioni Spread Spectrum; questo nome (che significa Spettro Sparpagliato) deriva dal fatto che se proviamo ad analizzare segnali modulati di questo tipo nel dominio della frequenza osserviamo uno spettro quasi piatto che si confonde molto bene con il rumore.
Un fatto interessante è che la correlazione con segnali diversi da quello iniziale dà luogo a un andamento senza picchi pronunciati (vedi figura 4). Quindi questa tecnica è molto utile per trasmettere contemporaneamente più segnali in modo che non si disturbino a vicenda (vedi [6]); ogni ricevitore deve essere opportunamente istruito sul tipo di segnale che deve ricevere (Codice) per poter osservare il picco sulla correlazione.
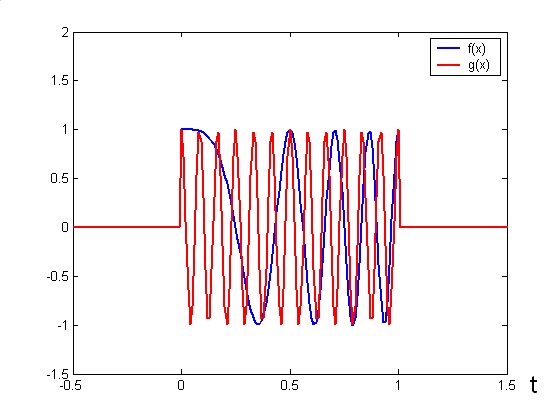
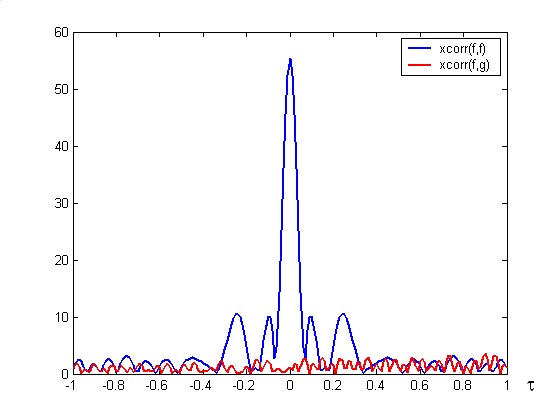
Figura 4 – Un chirp (f) e un segnale non modulato (g) danno luogo a una crosscorrelazione senza picchi
Bibliografia e Link
[1] Una risposta precedente molto esauriente sull’autocorrelazione
http://www.vialattea.net/esperti/php/risposta.php?num=8788
[2] Un sito con una utile applet con esempi di autocorrelazione
http://www.diit.unict.it/users/dpanno/webdit/icorr.htm
[3] Una precedente risposta sulla trasformata di fourier
http://www.vialattea.net/esperti/php/risposta.php?num=2308
[4] G.Picardi – Elaborazione del segnale Radar – Franco Angeli
[5] M.Skolnik – Introduction to radar systems – McGraw Hill
[6] Una precedente risposta sulle modulazioni Spread Spectrum
http://www.vialattea.net/esperti/php/risposta.php?num=8897
[7] P.Mandarini – Teoria dei segnali – Euroma
[8] Il libro on line di Alessandro Falaschi
http://infocom.uniroma1.it/alef/libro/html/libro/node161.html