Sviluppo in funzioni ortogonali.
Alcune classi di funzioni (ad esempio sotto ipotesi di esistenza, continuità e derivabilità a tratti in un certo intervallo) possono essere sviluppate come somma di infinite funzioni Φn(x)
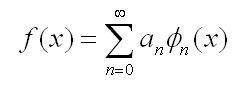
dove le funzioni Φn(x) formano un sistema completo di funzioni ortogonali, nel senso che, definito il prodotto scalare
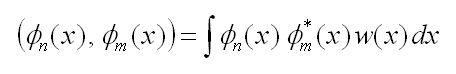 |
(1) |
dove w(x) è una certa funzione peso definita a priori nell’intervallo, si ha
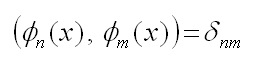
dove δnm è il simbolo di Kronecker, che vale 0 per n ≠ m e 1 per n = m. Analogamente ai vettori dello spazio euclideo, due funzioni il cui prodotto scalare sia nullo sono dette ortogonali.
Operativamente lo sviluppo in un dato sistema di funzioni ortogonali in un dato intervallo si ottiene semplicemente calcolando i coefficienti an, che possono essere ricavati direttamente dalla definizione del prodotto scalare,
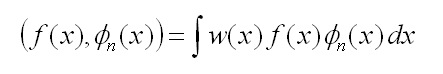
e inserendo nella definizione di prodotto scalare lo sviluppo
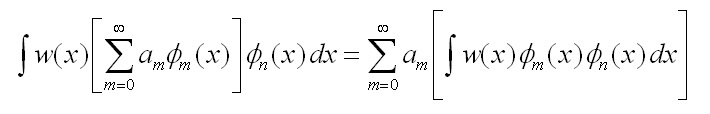
e per l’ortogonalità è diverso da zero solo il termine per m=n, si ha quindi l’espressione per il generico coefficiente:
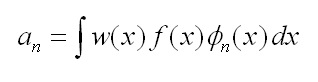
analogamente a quanto accade nello spazio Euclideo, in cui se un vettore generico v ha espressione v=(c1, c2, c3) significa che è formato dai vettori della base (u1, u2, u3) moltiplicati per i numeri c1, c2, c3;
v=c1 u1 + c2 u2 + c3 u3
e per conoscere il generico coefficiente ci basta moltiplicare scalarmente v per l’i-esimo vettore della base:
ci=v · ui
cioè prendere la proiezione del vettore v lungo la direzione ui.
La differenza, oltre che nella forma del prodotto scalare è che nello spazio Euclideo si hanno solo tre vettori nella base, mentre nel caso dei sistemi di funzioni ortogonali negli spazi funzionali la base è formata da infinite funzioni: (n=0, 1… ∞ ).
Utilità dello sviluppo in funzioni ortogonali.
Lo sviluppo in un sistema completo di funzioni ortogonali (base) è spesso molto utile nella soluzione delle equazioni differenziali. Gli sviluppi noti sono di solito legati a particolari equazioni differenziali, e ne costituiscono la soluzione generale.
Nel 1822 Fourier, trattando la trasmissione del calore, ha pubblicato lo sviluppo omonimo; poco più tardi i problemi di Hermite e di Sturm-Liouville hanno dato origine ai sistemi di polinomi di Hermite e Legendre rispettivamente, di grande importanza in molti campi della fisica: le armoniche sferiche ad esempio sono delle funzioni proporzionali ai polinomi di Legendre e rappresentano la soluzione in coordinate sferiche all’equazione di Schroedinger per l’atomo di idrogeno, sono cioè l’espressione matematica degli orbitali atomici.
Funzioni periodiche e Serie di Fourier.
Per la classe di funzioni periodiche di periodo T, per esempio, vale lo sviluppo in serie di Fourier (vedere anche la precedente risposta su vialattea [1]):
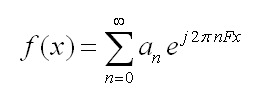 |
(2) |
dove le funzioni armoniche e j2 π nF x con (F = 1/T frequenza fondamentale) sono ortogonali nel senso della (1), con funzione peso pari a 1
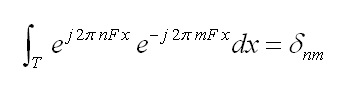
La serie di Fourier, grazie all’identità e jx = cos(x) + j sin(x) può essere scritta come in [1]:
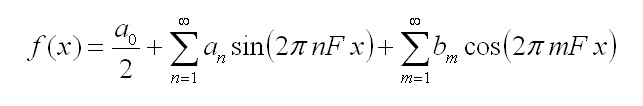
dove le funzioni sin(2 π nF x) e cos(2 π nF x) sono dette biortogonali nel senso che soddisfano alle
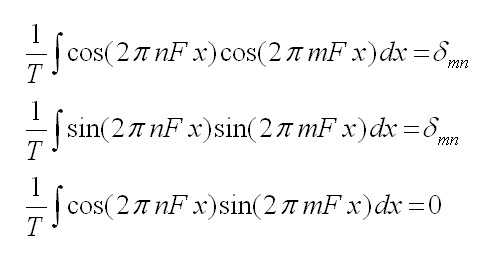 |
(3) |
I coefficienti an e bm sono calcolabili in maniera analoga a quanto fatto prima.
Funzioni sommabili e trasformata di Fourier.
Per la classe di funzioni Sommabili, cioè tali che la loro energia è finita:
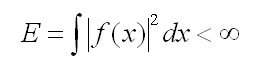
esiste la trasformata di Fourier, un’estensione della serie, in cui le funzioni armoniche
e j 2π fx
diventano un’infinità non numerabile, infatti la frequenza f ora può variare continuamente nel campo reale, e per ogni frequenza si ha un contributo infinitesimo.
Inoltre la definizione di ortogonalità assume la forma
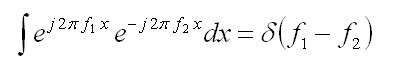 |
(4) |
in cui la δ(f) la delta di Dirac ha un significato simile al simbolo di Kronecker, è una specie di funzione (si chiama distribuzione) che è ovunque nulla, tranne che nel punto zero, dove assume un valore infinito, però mantenendo l’area pari ad 1.
La trasformata di Fourier è definita come
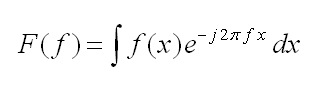 |
(5) |
Teorema di Parseval.
Il teorema di Parseval è intimamente legato al fatto che nello sviluppo le funzioni siano ortogonali, questo viene utilizzato nella dimostrazione (si veda [5]).
Il teorema di Parseval per le funzioni periodiche afferma che
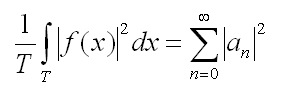 |
(6) |
cioè che la potenza della funzione periodica è anche pari alla somma delle ampiezze delle armoniche al quadrato; questo significa che le armoniche formano uno spettro di potenza del segnale;
per le funzioni sommabili
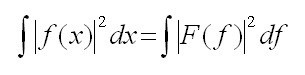 |
(7) |
e quindi
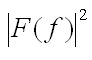
rappresenta lo spettro di densità di energia del segnale.
Riferimenti e Link
[1] Una risposta molto esauriente sulla serie di fourier
http://www.vialattea.net/esperti/php/risposta.php?numero=2308
[2] Sulla trasformata di fourier:
http://www.vialattea.net/esperti/php/risposta.php?num=3304
[3] Sulla DFT
http://www.vialattea.net/esperti/php/risposta.php?num=2966
[4] Eric W. Weisstein. “Complete Orthogonal System.” From MathWorld–A Wolfram Web Resource.
http://mathworld.wolfram.com/CompleteOrthogonalSystem.html
[5] Eric W. Weisstein. “Parseval’s Theorem.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/ParsevalsTheorem.html
[6] Paolo Mandarini – Teoria dei Segnali – EUroma