Leggendo la Vostra risposta sulla cicloide mi e’ venuta la curiosita’ di “visualizzare” la linea descritta da un punto su una sfera che ruoti senza slittamento su due dei propri assi con velocita’ differenti. Quale e’ l’equazione dove le due velocita’ di rotazione siano variabili (supponendo perpendicolari i due assi)?

Matematica  ·  GeometriaViews: 1503

L’equazione cercata dal lettore si ottiene applicando
una velocità angolare costante ai due parametri angolari del sistema
di coordinate sferiche illustrato in Fig. 1.

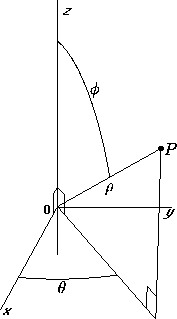
Fig. 1: Il sistema di coordinate sferiche

 

Mentre nel sistema di coordinate cartesiane un punto P
è identificato da una tripletta di valori (x,y,z), nel sistema
di coordinate sferiche un punto P è determinato da tre parametri
(r , q
, j )ove:

  • r indica
    la distanza tra l’origine degli assi cartesiani ed il punto P
  • q è
    il parametro che descrive l’angolo formato dall’asse x e dalla
    proiezione sul piano xOy del segmento OP
  • j è
    l’angolo formato dal segmento OP e l’asse z

Il sistema che consente di convertire coordinate sferiche
in cartesiane è il seguente:

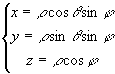
per ottenere il grafico del moto di un punto su una sfera
che ruoti su due assi perpendicolari, possiamo quindi sfruttare gli angoli
q , j
. Il primo rappresenta l’angolo di rotazione dell’asse
z, ed il secondo rappresenta l’angolo di rotazione dell’asse perpendicolare
contemporaneamente all’asse z ed alla proiezione del segmento PO
sul piano xOy.

La rotazione lungo gli assi scelti può essere rappresentata
assegnando delle funzioni con parametro temporale agli angoli q
, j che
rappresentino le velocità angolari w1 ed w2
dei due assi:

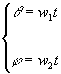
Ad esempio, assegnando velocità di rotazione nulla
per il primo asse e pari ad 1 Hz per il secondo asse

si ottiene l’equazione della circonferenza in Fig. 2 (nelle
figure, senza perdità di generalità, viene posto r
= 1)

 

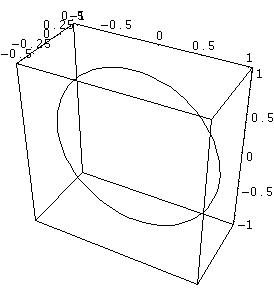
Fig. 2 : Grafico per w1 =
0, w2=1

La Fig. 3 rappresenta il percorso compiuto dal punto P
con velocità dei due assi pari ad 1Hz

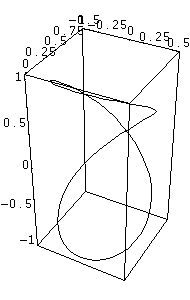
Fig. 3: Grafico per w1 =
1 w2=1

Composizioni più “fantasiose” si ottengono aumentando
la velocità di rotazione dei due assi e differenziandole. La Fig.
4 mostra il percorso del punto P con frequenze di rotazione di
3Hz ed 1Hz, sui due assi, rispettivamente.

 

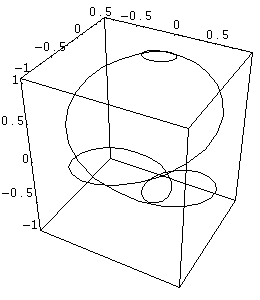
Fig. 4: Grafico per w1 =
3, w2=1

Note

I grafici di questa pagina sono stati ottenuti con Mathematica utilizzando
le seguenti istruzioni:

x[t_]:=R*Cos[theta[t]]*Sin[phi[t]]
y[t_]:=R*Sin[theta[t]]*Sin[phi[t]]
z[t_]:=R*Cos[phi[t]] eq[t_]:={Cos[theta[t]]*Sin[phi[t]],Sin[theta[t]]*Sin[phi[t]],Cos[phi[t]]}

theta[t_]:=3t
phi[t_]:=t
R=1
ParametricPlot3D[eq[t], {t, 0, 2*Pi}]