I numeri immaginari,
che si rappresentano nella forma ai dove a è un numero reale (positivo o negativo)
e i l’unità immaginaria, sono
utilizzati in algebra in tutti i calcoli in cui compaiono estrazioni
di radici, di indice pari, di numeri reali negativi.
Es. 
3i
= 4i
=
i
………………………
Il
simbolo i è, quindi, utilizzato
al posto di 
.
Tali
numeri si sommano e moltiplicano
tra loro alla stessa maniera degli altri numeri nel rispetto delle leggi
e proprietà che regolano le operazioni tra questi.
Così
si avrà che, ad esempio :
i2 = -1 ; i3 = i2 x i = -i ; i4 = i2 x i2 = 1 ; i5
= i
; ecc.
ai + bi = (a
+ b)i ;
ai x bi = abi2 = ab
= – ab
ai x (bi + ci) = ai
x bi
+ ai x ci
= – ab – ac
ecc.
Da
un punto di vista puramente formale i numeri immaginari agevolarono enormemente
l’esecuzione del calcolo algebrico sin dalla loro prima apparizione
nel XVII secolo se si tiene conto del simbolismo fino allora adottato
piuttosto “pesante” rispetto all’attuale.
L’introduzione del simbolo i, cui si dà il significato e con cui si opera come abbiamo detto,
ha consentito l’ampliamento del campo dei numeri reali con il campo dei numeri complessi v definiti come somma di un numero immaginario bi e
un numero reale a: v = a + bi. (Per inciso, il numero
complesso 
= a – bi è detto coniugato di v e il numero reale v=
si chiama modulo
di v)
In
tal modo tutti gli altri numeri non sono che numeri complessi particolari.
Ad
esempio, un numero reale è un numero complesso con b = 0 e un numero immaginario è un numero complesso con
a = 0.
Nel
campo dei numeri complessi si
possono, a questo punto, effettuare tutte le operazioni fondamentali e
le loro inverse (addizione, sottrazione, moltiplicazione, elevazione a
potenza, divisione) senza avere necessità di inventare altro tipo di numero
o simbolo.
Nel
campo complesso è possibile affermare allora che “Ogni equazione algebrica a
coefficienti complessi di ordine n qualsiasi ammette n soluzioni complesse
(non necessariamente tutte distinte)”.
Tale
teorema non è valido se riferito al campo reale; nel senso che non si può affermare che “Ogni equazione algebrica a coefficienti reali di ordine n qualsiasi ha
n soluzioni reali (non tutte necessariamente distinte)”.
Però
grazie ad esso possiamo, ad esempio, affermare che “Ogni equazione algebrica a
coefficienti reali di ordine n dispari ammette almeno una radice reale”
cosa che non avremmo potuto fare senza l’ampliamento del campo reale
con i numeri complessi.
Anche
in geometria analitica
vengono considerati enti immaginari con la stessa finalità accennata per
l’algebra (d’altra parte la geometri analitica non fa altro che tradurre
in algebra enti e relazioni geometriche).
Così
punti immaginari (o complessi) sono caratterizzati dall’avere almeno una
coordinata complessa.
Le
rette immaginarie sono rappresentate da equazioni lineari a coefficienti
complessi come ad esempio la retta y = ix + 1 che è perpendicolare a se
stessa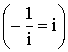 
Altra
interessante utilizzazione dei numeri complessi avviene nel calcolo vettoriale dove un vettore
v(a,b), di componenti a e b
in un riferimento cartesiano Oxy e di modulo v=
, si identifica
col numero complesso v = a + bi (avente lo stesso modulo) e tutte le operazioni fra vettori si traducono
in operazioni tra numeri complessi.