Prima di rispondere al lettore è opportuno esporre
una serie di precisazioni.
Dato un sistema di riferimento, un sottoinsieme di
punti nello spazio n-dimensionale può essere
descritto in forma generale mediante una equazione,
funzione o proposizione nel sistema di riferimento
prescelto.
La forma in cui viene espressa l’equazione
o proposizione che definisce i punti nel piano viene
definita
- implicita, se l’equazione è del tipo
f(x1,…,xn)=0 - esplicita, se l’equazione è del tipo
xn=g(x1,…,xn-1)
- parametrica, se (x1,…,xn)=(
x1(t),…,xn(t)),
ovvero l’n-pla di coordinate è scrivibile
come funzione del solo parametro t
ciò indipendentemente dal sistema di
coordinate utilizzato.
Si consideri, ad esempio, lo spazio bidimensionale (il
piano) e la circonferenza con centro
nell’origine del sistema di riferimento e raggio r.
La fig. 1 illustra le tre forme dell’equazione per i
sistemi di riferimento cartesiano e polare.
| Sistema di Riferimento |
Forma | Equazione |
| Cartesiano | implicita | x2+y2=r2 |
| Cartesiano | esplicita | n.d. |
| Cartesiano | parametrica | (R Cos(t),R Sin(t)) |
| Polare | implicita | R – r = 0 |
| Polare | esplicita | R = r |
| Polare | parametrica | (r, t) |
Fig. 1:
Equazione della circonferenza di raggio r in forme
e sistemi di riferimento vari
In fig. 1 R e t sono è la variabili che
esprimono il raggio e l’angolo di riferimento per le
coordinate polari, x e y le variabili di
ascissa ed ordinata del piano cartesiano, mentre r è
una costante (il raggio della circonferenza). Si osservi
che la forma esplicita y=f(x) dell’equazione
della circonferenza non è disponibile perché la
funzione f non è analitica, mappando valori
dell’ascissa in coppie di ordinate (le
determinazioni positiva e negativa della radice
quadrata).
Come si evince dalla fig. 1, la scrittura della forma
parametrica di un equazione in coordinate polari
R = f(t) è (f(t),t).
Se ho ben interpretato la domanda, ciò che interessa
al lettore è un processo per scrivere un equazione in forma
parametrica in coordinate cartesiane, a partire dalla
forma esplicita in coordinate polari. Il procedimento
consta di una semplice conversione tra i due sistemi di
coordinate. Si consideri la Fig. 2.
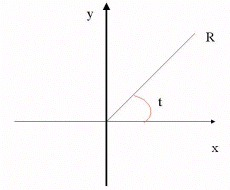
Fig.2: Sistema di
riferimento cartesiano e polare
La conversione tra coordinate polari e cartesiane
consiste nel determinare una coppia di valori (x,y)
per ogni coppia (R,t), mediante
x = R cos(t), y = R sin(t)
Riassumendo, per scrivere l’equazione parametrica
in coordinate cartesiane a partire dall’espressione
della forma esplicita in coordinate polari si opera come
segue:
- sia R = f(t) l’equazione in forma
esplicita in coordinate polari - (R, t) = (f(t), t) è l’equazione
parametrica in coordinate polari - si converte l’ultima espressione in
coordinate cartesiane ottenendo
( f(t) cos(t), f(t) sin(t) )
![]()
Applichiamo ora il metodo al Folium di Descartes,
- l’equazione in forma esplicita in coordinate
polari è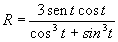
- la forma parametrica (in coordinate polari) è
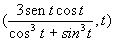
- in coordinate cartesiane
![]()
ove l’equazione polare si ottiene sostituendo x
= R cos(t), y = R sin(t) nell’equazione
implicita del Folium
x3+y3-3xy
= 0
Proviamo quindi a tracciare il Folium con Mathematica:
In[1] =
r = 3 Cos[t]
Sin[t]/(Cos[t]^3+Sin[t]^3);
In[2] =
ParametricPlot[{r Cos[t], r
Sin[t]}, {t, 0.01, 2 Pi}]
il cui risultato è in figura 3
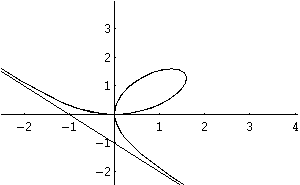
Fig.3: Folium di
Descartes tracciato con Mathematica
Si osservi che il motore grafico del Mathematica
interpreta erroneamente come connessi i due punti
all’infinito, la figura va quindi intesa senza la
retta che passa per i punti (-1, 0) e (0, -1).
Ancora un’ultima osservazione: ovviamente, la
forma parametrica proposta dal metodo non è l’unica
possibile. L’equazione parametrica
“ufficiale” del Folium nel sistema di
riferimento cartesiano è
(3 a t/(1+t3), 3 a t2/(1+t3)
)
ove a è un parametro di scala reale positivo.