Una funzione analitica che consenta di scrivere il proprio
nome, qualsiasi esso sia, non esiste.
Si immagini di voler rappresentare la lettera B con una
funzione analitica tipo y=f(x), nel piano xOy.
In alcuni tratti, la lettera dovrebbe essere rappresentata
graficamente da una funzione che assume tre valori contemporaneamente,
il che la rende non analitica.
I font True Type sono stati definiti su uno standard
vettoriale, cioè basato sulla composizione di elementi grafici
nel piano. L’approccio qui illustrato è solo un esempio di composizione
vettoriale di font. Gli standard vettoriali moderni, come True Type,
Postscript, seguono un procedimento simile e consentono di scalare
e trasformare i caratteri grafici a piacimento, convertendoli in immagini
bitmap. La costruzione degli elementi grafici è spesso frutto
di un calcolo che coinvolge operazioni numeriche complesse, specialmente
applicando stili come il corsivo e il grassetto. Per ridurre
il sovraccarico computazionale, stampanti e computer ricorrono alla cache,
una porzione della memoria di sistema o di massa dove registrare temporaneamente
le immagini ottenute dalla composizione degli elementi grafici, per poi
richiamarle ad ogni riutilizzo.
Definiamo quindi il nostro insieme di elementi vettoriali.
Ricorrendo alla composizione funzioni parametriche, e
alla loro rappresentazione nel piano, è possibile costruire algoritmicamente
una lettera tramite l’unione dei seguenti elementi grafici:
- La circonferenza di raggio R : (Rcos(t),
Rsin(t)), 0 £ t £
2p
- Il segmento verticale lungo l: (0,t), 0 £
t £ l
- Il segmento orizzontale lungo l : (t,0),
0 £ t £ l
- Il segmento diagonale a 45° ascendente, lungo l
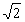 :
:
(t,t), , 0 £ t £
l
- Il segmento diagonale a 45° discendente, lungo l
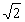 :
:
(t,-t), , 0 £ t £
l
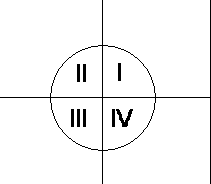
Fig. 1 : Suddivisione del piano in quattro
quadranti
E’ possibile tracciare porzioni di circonferenza modificando
l’intervallo di variazione del parametro t per i quattro quadranti
del piano (cfr. Fig. 1):
- Quadrante I : 0 £ t
£ p /2
- Quadrante II : p
/2£ t £ p
- Quadrante III : p
£ t £ 3/2p
- Quadrante IV: 3/2p £
t £ 2p
Per costruire una lettera è necessario comporre
i diversi elementi che la costituiscono. Tale composizione può
avvenire per traslazione, che si ottiene aggiungendo alle ascisse ed ordinate
la quantià (Xc, Yc) voluta.
Ad esempio:
- circonferenza di raggio R e centro (Xc,
Yc) : (Xc, Yc) + (Rcos(t), Rsin(t)), 0 £
t £ 2p
Infine, è possibile applicare un fattore di scala
A a tutti gli elementi grafici moltiplicando l’equazione parametrica
per il fattore di scala A.
Ad esempio;
- Ingrandimento del 50% : A=1.5
- Riduzione del 30% : A = 0.7
- Circonferenza di raggio R ridotta del fattore
A : (ARcos(t),A Rsin(t)) , 0 £
t £ 2p
Ogni lettera sarà quindi composta di più
elementi e potrà essere tracciata mediante un algoritmo
che li disegni in successione. La lettera B di figura 2 potrebbe essere
composta da tre elementi:
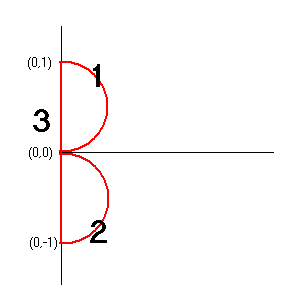
Fig 2: Costruzione della lettera B
- Elemento 1: Semicirconferenza di centro (0,1/2)
e raggio 1
- Elemento 2: Semicirconferenza di centro (0,-1/2)
e raggio 1
- Elemento 3: Segmento verticale lungo 2 e traslato
in (0,-1)
Ogni volta che desideriamo tracciare la lettera dobbiamo
invocare l’algoritmo che compone i tre elementi costitutivi. Seguendo
un approccio simile è possibile definire tutte le lettere dell’alfabeto
ed i numeri e la stesura di un intero testo corrisponde ad una invocazione
in sequenza degli algoritmi di composizione delle singole lettere.
Non
sono d’accordo con questa risposta. Non è per nulla necessario,
affinché la funzione disegni lettere e cose simili, che vi siano molte
soluzioni per ogni x. Basta che f(x) fornisca, ad
esempio, per un certo intorno
I(x0 – n, x0 + n)
(dove n è un numero “piccolo” a piacere) soluzioni riguardanti
la parte superiore di una “O”. Poi, in
I(x0 + n, x0 + 2n)
dà soluzioni che formano la parte inferiore, e ancora in
I(x0 + 2n, x0 + 3n)
dà di nuovo soluzioni per la parte superiore ecc… È evidente
che se n è un numero sufficientemente piccolo, sarè
impossibile distinguere l’intrinseca discontinuità della funzione ad
“occhio nudo”. Pensandoci, nemmeno l’inchiostro di una penna è
“continuo” nel senso matematico del termine, ma nessuno se ne preoccupa,
perché funziona. Matematicamente, dunque, la funzione è salva,
perché ad ogni x corrisponde una sola y, ma
“visivamente” il risultato è proprio una scritta con x che
sembrano fornire più y. La domanda che potrebbe sorgere
spontanea è: esiste una funzione del genere? Personalmente, ne ho
ideata una, che si basa interamente su una particolare serie di funzioni
segno. Se vi interessa posso spedirvi il documento in cui la spiego (anche
se è un po’ ingombrante). Ci ho anche scritto “Buon Natale”! Ora
però ecco la domanda che volevo porvi: se il numero n piccolo a
piacere tendesse a 0, cosa succederebbe alla funzione? Cioè, se,
preso un qualsiasi intervallo qualunque di x, il “numero di
alternanze” della funzione da una y ad un’altra tendesse ad infinito,
che accadrebbe? Forse però sono discorsi campati in aria: se potessi
spedirvi la funzione sarebbe tutto molto più chiaro. Grazie.
(risponde
È
teoricamente possibile costruire una sequenza di funzioni fortemente
discontinue, tali che traccino il contorno di lettere.
Esattamente, la risposta precedente asseriva che non è possibile
scrivere *una* funzione analitica che tracci il proprio nome, e nemmeno
alcune lettere. È viceversa possibile scrivere una serie di
funzioni – perlopiù parametriche – che, tracciate in sequenza
opportuna, abbiano come grafico le lettere dell’alfabeto.
Per rispondere all’ultima domanda del lettore, se n tende a zero
la serie di funzioni trovate si riduce a quella parametrica, con la
differenza che mantiene la discontinuità.
Buon Natale anche a tutti i lettori di ViaLattea.