Spiegare in due parole l’equazione di Schrödinger
è veramente un’impresa da titani. Per avere almeno
una minima idea di quello di cui si sta parlando è
necessario spendere due parole sulla natura ondulatoria
della materia.
E’ noto che particelle materiali
esibiscono proprietà di onde. La lunghezza d’onda
connessa con una particella è associabile al suo momento
p, cioè al prodotto massa*velocità (p=mu),
ed è espressa dalla relazione (essendo h la costante di
Planck)
![]()
E’ comprensibile che un discorso del genere possa
lasciare disorientati. Come può un elettrone (o un
fotone) essere contemporaneamente sia un’onda che
una particella? Il fatto è che probabilmente essi non
sono nessuna delle due cose. Semplicemente si comportano
come onde in determinate condizioni e come particelle in
altre. La cosa importante è però che il loro
comportamento può in ogni caso essere descritto in
termini di una funzione d’onda ![]() .
.
Ragionare in termini di funzioni d’onda è dunque il
modo più soddisfacente per descrivere sistemi di questo
tipo.
Vediamo di che si tratta.
Scriviamo l’equazione di
un’onda armonica che si propaga in direzione degli x
positivi con velocità u. Essa, nel punto x
e al tempo t, è data da
![]()
[tenendo presente che exp(ix) = cosx +
i senx]
Si può facilmente verificare che un’onda di
questo genere è periodica nel tempo (con periodo ![]() )
)
e nello spazio (con periodo ![]() ). Cioè aumentando
). Cioè aumentando
t di T o x di ![]()
sia ![]() che le sue derivate rimangono invariate.
che le sue derivate rimangono invariate.
Inoltre, dato che l’esponenziale, in valore
assoluto, non può mai superare il valore di 1,
l’oscillazione avviene al massimo tra +A e -A.
Il parametro A è dunque l’ampiezza
dell’onda.
Importante è anche il teorema di
Fourier. Esso dice che un’onda di una determinata
frequenza può essere ricostruita dalla combinazione di
un pacchetto di onde a frequenza variabile e di adatta
ampiezza
![]()
In generale per rappresentare una particella in movimento
sarà necessario costruire un’onda localizzata. Un
tale tipo di onda può essere costruita scegliendo
opportunamente il pacchetto d’onde in modo che esse
interferiscano costruttivamente in un punto e
distruttivamente in tutti gli altri. Il pacchetto
d’onde in questione sarà caratterizzato da un range
molto stretto di numeri d’onda e quindi può essere
virtualmente considerato omogeneo in frequenza.
Supponiamo ora che un elettrone libero
che viaggia in direzione degli x positivi con
momento p = mu ed energia cinetica
![]()
sia rappresentato dalla funzione
![]()
Operando le opportune sostituzioni ed
essendo
![]()
si può arrivare a verificare che la
funzione d’onda ![]() descritta sopra è soluzione
descritta sopra è soluzione
dell’equazione differenziale
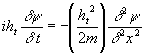
Questa è l’equazione di
Schrödinger per un elettrone libero che si muove in uno
spazio monodimensionale. L’estensione al caso
tridimensionale è immediata se si esprime l’energia
come
![]()
. 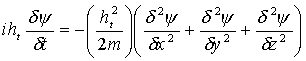
o, con la usuale simbologia
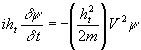
Fin qui abbiamo parlato di una particella
libera.
Diverso è però il caso di una
particella che si muove sotto l’influenza di un
campo esterno. Nell’energia sarà necessario
introdurre un termine energia potenziale assunto
dipendente solo dalle coordinate. Si avrà dunque che
![]()
e quindi
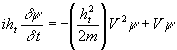
Se a questo punto definiamo
l’operatore Hamiltoniano H come
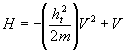
possiamo scrivere che
![]()
In pratica l’operatore Hamiltoniano è un
operatore che, applicato ad una generica ![]() , ne
, ne
restituisce una derivata seconda rispetto alle coordinate
spaziali sommata del valore di ![]() stessa moltiplicata
stessa moltiplicata
per il potenziale.
Questa è l’equazione di Schrödinger dipendente
dal tempo per una particella di energia potenziale
potenziale V(x,y,z) che si muove
tridimensionalmente. Tale equazione, così costruita, ha
la caratteristica di essere lineare; cioè se ammette una
soluzione ![]() ammette anche una soluzione
ammette anche una soluzione ![]() ,
,
ove c è una costante arbitraria diversa da
zero.
Inoltre la funzione |![]() |2 ha la caratteristica
|2 ha la caratteristica
di rappresentare la probabilità di trovare la particella
in un determinato elemento di volume dxdydz al
tempo t. Dato che la probabilità di trovare la
particella in qualsiasi parte dello spazio al tempo t
deve essere unitaria, è necessario che l’integrale
di |![]() |2 su tutto lo spazio dia 1. Una
|2 su tutto lo spazio dia 1. Una
funzione ![]() che corrisponda a questa
che corrisponda a questa
caratteristica si dice normalizzata.
In molti casi particolari è possibile
scindere la funzione d’onda ![]() in una parte f
in una parte f
dipendente dal tempo e in una parte ![]() dipendente
dipendente
dalle coordinate.
![]()
dove si ha che
![]()
(equazione di Schrödinger indipendente
dal tempo)
e
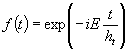
Questi casi particolari giocano un ruolo fondamentale
nello sviluppo delle teorie sulle strutture atomiche in
quanto descrivono gli stati stazionari nei quali la
dipendenza dal tempo influenza solamente la fase.
Ma torniamo all’operatore Hamiltoniano.
Fino ad ora si è discusso sull’equazione di
Schrödinger. Si è detto che l’equazione di
Schrödinger è una equazione differenziale le cui
soluzioni descrivono nel tempo e nello spazio
“entità” in movimento quali possono ad esempio
essere gli elettroni di un atomo. Risolvere tale
equazione, ove sia possibile, permette di risalire alle
mappe di densità elettronica che descrivono la
probabilità di trovare gli elettroni in determinati
punti dello spazio.
L’equazione di Schrödinger è una equazione agli
autovalori. Cosa significa?
Una generica equazione agli
autovalori
![]() [dove O è per esempio
[dove O è per esempio
l’operatore a (d/dx2) + b (d/dx) + c]
assume soluzioni di una data classe (importanti sono
quelle continue, normalizzabili, ed a valor singolo) solo
quando il parametro E assume certi specifici valori
numerici. Tali valori numerici sono detti autovalori mentre
le corrispondenti soluzioni sono le autofunzioni
dell’operatore O.
Supponiamo di disporre di una terna di
autofunzioni ![]() aventi autovalore E ed
aventi autovalore E ed
appartenenti alla classe descritta sopra. Allora anche
una qualsiasi loro combinazione lineare ![]() sarà
sarà
una autofunzione appartenente alla medesima classe ed
avente autovalore E. Questa regola è quella che
definisce uno spazio vettoriale. In generale in uno
spazio ad n dimensioni il numero massimo di
vettori linearmente indipendenti è n e quindi
qualsiasi vettore sarà sempre ottenibile da una
combinazione lineare di n vettori. Al tendere di n
all’infinito si ottiene uno spazio
infinito-dimensionale che è detto spazio di Hilbert.
Qualsiasi spazio finito ottenibile per esempio dalle
autofunzioni di un operatore con autovalore E è
dunque un sottospazio dello spazio di Hilbert.
Ecco allora che sulla base di quanto detto possiamo
riassumere che l’equazione di Schrödinger è una
equazione agli autovalori, che consente dunque soluzioni
della stessa classe solo in corrispondenza di determinati
valori dell’autofunzione E.
In particolare perché le soluzioni siano utilizzabili
ai fini di una rappresentazione atomica è necessario che
esse siano normalizzabili, continue ed a valor singolo.
Soluzioni di questo tipo sono ottenibili solo in
corrispondenza di determinati valori di E, ciascuno dei
quali rappresenta l’energia complessiva del sistema
in una determinata configurazione.
Detta in termini molto semplificati si può dire
quindi che per ciascun livello di energia (per ciascun
autovalore E) l’operatore Hamiltoniano è
quell’operatore che fornisce una serie di
autofunzioni (che sono quindi soluzioni
dell’equazione) che rappresentano la popolazione
elettronica corrispondente a quella energia.
Per concludere bisogna tuttavia dire che nella pratica
una soluzione dell’equazione di Schrödinger è
possibile solo in casi semplici, mentre nella maggior
parte dei casi si fa ricorso a soluzioni che sono frutto
di innumerevoli compromessi e semplificazioni. Solo col
continuo progredire degli strumenti di calcolo sarà
possibile estendere la risoluzione rigorosa a casi sempre
più complessi.