Il problema alla base della domanda, quello cioè
della probabilità che almeno due in un gruppo di persone festeggino il
compleanno lo stesso giorno, è un’applicazione classica della formula
della probabilità di eventi indipendenti. Tale formula è
già stata esposta in una precedente risposta di Carlo
Consoli in questa stessa sezione.
In analogia e a
completamento di quanto esposto nella risposta citata, possiamo calcolare la
probabilità P1(p) che due persone in un
gruppo di p compiano gli anni lo stesso giorno cercando la
probabliltà che ciò non accada. Ragioniamo quindi in
questo modo: indipendentemente dalla data del compleanno della prima persona,
ci sono 364 casi su 365 in cui il secondo compie gli anni in un giorno
diverso; ancora indipendentemente, poi, ci sono 363 casi su 365 in cui il
terzo compie gli anni in un giorno diverso da entrambi i precedenti, e
così via. La probabilità che i compleanni cadano in date tutte
diverse è quindi
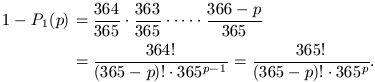
Calcolando esplicitamente tale valore (ad esempio) per
p = 30, si trova proprio che la probabilità di avere
almeno due compleanni coincidenti in un gruppo di trenta persone è
pari circa al 70.63%.
Allo stesso risultato si
può tuttavia arrivare, come sempre, contando il numero dei casi
favorevoli e il numero dei casi possibili. Le possibili disposizioni di
p date su 365 sono infatti 365p, mentre quelle senza
ripetizioni sono
365 (365 – 1) 



 (365 – p + 1)
(365 – p + 1)
= 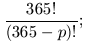
ricordando allora che la probabilità di un evento, in
ipotesi di equiprobabilità, è pari al rapporto tra il numero
dei casi favorevoli e il numero dei casi possibili, si ritrova la formula
vista sopra. Si noti che procedendo in questo modo abbiamo tenuto conto
dell’ordine in cui le varie date vengono “sorteggiate”; avremmo potuto anche
non tenerne conto ma questo avrebbe voluto dire dividere per p! sia il
numero dei casi favorevoli sia il numero dei casi possibili e, quindi,
avrebbe portato ancora una volta allo stesso risultato.
Il metodo del conteggio
dei casi favorevoli, che come si è visto non è indispensabile
per calcolare la probabilità di avere almeno due compleanni
coincidenti, può diventare invece molto utile in casi complicati come
quello che stiamo esaminando. Cerchiamo allora di ricalcolare la
probabilità di avere almeno due compleanni coincidenti cercando di
ragionare sulle estrazioni di p date e trascurando l’ordine di
estrazione. Di qui in avanti indicherò con a il numero di
giorni di un anno: oltre a rendere un po’ più leggibili le notazioni,
almeno a mio parere, tale scelta permette di applicare la formula che
otterremo sia agli anni non bisestili con a = 365 sia a
quelli bisestili con a = 366. Il numero totale di
estrazioni possibili (eliminando l’effetto dell’ordine) è così
ap / p! e quello di estrazioni senza ripetizioni
è
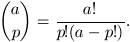
Per contare il numero di estrazioni con una (e una sola)
ripetizione ragioniamo così: ci sono a possibili scelte per le
due date uguali, dopo di che tutte le altre p – 2 devono
essere diverse da questa, cioè costituire un sottoinsieme senza
ripetizioni tratto da un insieme di a – 1 elementi. È
inoltre abbastanza immediato capire che ogni estrazione costruita in questo
modo è diversa da tutte le altre, cioè che non stiamo “contando
due volte” la stessa estrazione: il numero da noi cercato è allora
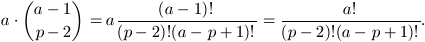
La questione si complica quando si cerca di calcolare il
numero di estrazioni con più ripetizioni. Consideriamo, per esempio,
il caso in cui quattro date sono uguali a due a due. Dobbiamo allora
scegliere un qualsiasi sottoinsieme di 2 elementi (le date che si
ripeteranno) e assegnare le altre p – 4 date in modo che
formino un sottoinsieme senza ripetizioni delle rimanenti
a – 2 date. Anche contando in questo modo stiamo
considerando una sola volta tutti i casi possibili, per cui il numero di
estrazioni con due date “doppie” è
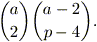
Contiamo adesso il numero di estrazioni in cui la
ripetizione oppure le due ripetizioni si trovano in un qualsiasi sottoinsieme
di date formato da g elementi. È abbastanza facile capire che
nel caso di ripetizione singola basta scegliere le due date uguali in
g possibili modi e le altre p – 2 in modo che formino
un sottoinsieme senza ripetizioni tratto da un insieme di
a – 1 elementi: il numero di estrazioni con una ripetizione
all’interno del sottoinsieme che ci interessa è quindi
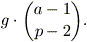
Nel caso di due ripetizioni doppie bisogna essere molto
cauti: infatti, non è necessario che entrambe le date ripetute
cadano nel sottoinsieme che ci interessa. Il numero di casi favorevoli in
questa situazione si calcola allora considerando g scelte per la prima
data e a – 1 scelte per la seconda, assegnando poi le altre
p – 4 date in modo che formino un sottoinsieme senza
ripetizioni delle rimanenti a – 2 date. Attenzione ancora,
però: in questo modo stiamo contando due volte le estrazioni in cui
entrambe le date ripetute cadono effettivamente nel sottoinsieme in esame e
quindi dovremo sottrarre tale numero dal conto. Otteniamo dunque che il
numero di estrazioni favorevoli è
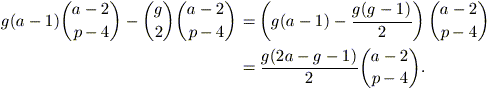
Calcoliamo finalmente le probabilità condizionate che
ci interessano. Data la presenza di una singola ripetizione, la
probabilità che essa avvenga all’interno del sottoinsieme di date in
considerazione è
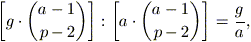
come l’intuizione potrebbe in effetti suggerire in un primo
momento. Nel caso più complicato, però, si ha una
probabilità condizionata pari a
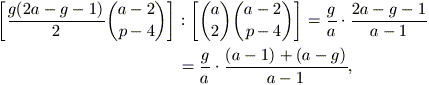
che è strettamente maggiore di
g / a e addirittura (anche se forse in un primo
momento questo potrebbe fare violentemente a pugni con la stessa intuizione
di cui sopra) è tanto più distante da
g / a quanto più g è piccolo.
Questo dipende però dal fatto che la probabilità che
almeno una di due date casuali cada un in certo sottoinsieme è
molto maggiore della probabilità che ci cada una singola data.
Credo che gli esempi visti fin qui possano essere
sufficienti per concludere che la probabilità che in un gruppo di
p persone si celebrino (almeno) due compleanni all’interno di un
periodo di g giorni è strettamente maggiore di
g / a volte la probabilità che all’interno di
un gruppo di p persone vi siano (almeno) due compleanni coincidenti.
Per confermare questa impressione, ho condotto una simulazione iterativa
della situazione di un gruppo di 30 persone, approssimando numericamente la
probabilità di avere due (o più) compleanni sia senza
condizioni sulla data sia a condizione che tale coincidenza avvenga entro un
periodo di 36 giorni (approssimativamente pari a un decimo della durata
dell’intero anno). Le frequenze delle coincidenze ottenute sono tra il
70.34% e il 70.96% nel primo caso (si ricordi che il valore teorico è
circa del 70.63%) e tra il 10.56% e il 10.81% nel secondo caso, quindi
notevolmente superiore a un decimo della probabilità “non vincolata”.
Penso che si sia anche
capito, vista la strada da seguire per calcolare tale probabilità, che
non è sperabile di ottenere una formula generale esplicita semplice e
compatta come quella vista sopra per il caso non vincolato: la
probabilità cercata va calcolata caso per caso a seconda del numero di
persone che compongono il gruppo esaminato.