I logaritmi e Napier
Definizione: Dati due numeri positivi a e
b, con a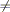 
1, si chiama
logaritmo in base a del numero b e si indica con
logab l’unica soluzione dell’equazione
ax = b.
La definizione di limite permette di affermare che:
Ogni numero reale positivo b si può scrivere, in modo unico, come
potenza di un altro qualsiasi numero a positivo, diverso da 1.
L’insieme di tutti i
numeri positivi, rispetto a una data base a, si chiama sistema dei
logaritmi a base a. Esistono naturalmente, infiniti sistemi di
logaritmi, perché infinite sono le possibili basi (cioè tutti i
numeri positivi diversi da 1). Tra questi infiniti sistemi di logaritmi, due
sono quelli che comunemente si considerano, e precisamente:
-
quello a base e, numero irrazionale (detto numero
di Nepero), il cui valore approssimativo è 2.71828…; tale
sistema è detto sistema dei logaritmi naturali o neperiani. -
quello a base 10 detto sistema dei logaritmi
decimali, o volgari, o di Briggs.
John Napier (o Giovanni Nepero) era un ricco
proprietario terriero che passava il suo tempo amministrando i suoi vasti
possedimenti e scrivendo su svariati argomenti. Per Napier lo studio della
matematica fu solo un passatempo. Tra i numerosi contributi matematici da
lui forniti vi è un metodo mnemonico per alcune formule applicate alla
trigonometria sferica, note come le “analogie di Napier” o la
“regola delle parti circolari di Nepero“. Descrisse un metodo di
moltiplicazione che impiegava dei bastoncini di sezione quadrata detti
bastoncini di Nepero.
La discussione di
Napier sui logaritmi apparve nel 1614 nell’opera Mirifici logarithmorum
canonis descriptio (Descrizione della regola meravigliosa dei
logaritmi). Va ricordato che diversamente dai logaritmi in uso oggi, i
logaritmi di Napier sono a base 1 / e e comprendono la costante
107.
Spieghiamo molto
semplicemente l’idea centrale su cui si basa l’invenzione di Napier. Per
mantenere molto vicini tra loro i termini di una progressione geometrica
delle potenze intere di un dato numero è necessario assumere come
numero dato una cifra molto vicina all’uno. Appunto per questo Napier decise
di usare come suo numero di base 1 – 10-7 (ossia
0,9999999). Ora i termini della progressione delle potenze crescenti sono
troppo vicini tra loro. Per ottenere un maggiore equilibrio e per evitare
cifre decimali Napier pensò di moltiplicare ciascuna potenza per
107. Ossia: consideriamo il numero N; se
N = 107[(1 – 1 / 107)]L
allora L è il logaritmo neperiano di
N. Così, il logaritmo di 107 è 0, quello di
107[(1 – 1 / 10)]7 è 1 e via
dicendo. Se egli avesse diviso per 107 i numeri e i logaritmi si
sarebbe ottenuto un sistema di logaritmi con la base 1 / e.
Napier confidava che i
suoi logaritmi avrebbero fatto risparmiare molto tempo agli astronomi e li
avrebbero liberati dagli insidiosi errori di calcolo. Duecento anni
più tardi, Laplace sarebbe stato d’accordo, sostenendo che i
logaritmi allungano la vita all’astronomo, accorciandone il lavoro.