Le equazioni differenziali (ED) sono un tipo di equazione in cui le incognite sono funzioni, e in cui compaiono le derivate della funzione incognita. Se c’è una sola variabile indipendente, le equazioni sono dette ‘totali’ o ‘ordinarie’. Se altrimenti le variabili indipendenti sono più di una l’equazione è detta alle derivate parziali. L’ordine di una ED è dato dall’ordine più alto della derivata che compare nell’equazione stessa.
Premetto inoltre che, essendo l’operazione di integrazione di una funzione un’operazione non risolubile in generale (al contrario della derivazione, ad esempio), il problema della risoluzione di un’equazione differenziale, sia essa ordinaria o alle derivate parziali, si considera risolto quando è dimostrata l’esistenza (e magari anche l’unicità) della soluzione, anche se non si riesce a trovarla esplicitamente! Naturalmente, da un punto di vista applicativo, conoscere una soluzione, anche se approssimata, è spesso fondamentale per poter trarre conclusioni sul sistema che quella stessa equazione descrive.
Infine, l’equazione è detta lineare se la variabile dipendente (cioè l’incognita) e le sue derivate compaiono tutte al massimo a potenza unitaria. In tal caso, si dimostra che ogni combinazione lineare di soluzioni dell’equazione è soluzione anch’essa. Ad esempio:
è una equazione differenziale ordinaria lineare del terzo ordine. Se sostituiamo by con by3 l’equazione diventa non lineare, a causa della presenza del cubo della variabile dipendente y.
L’equazione delle onde è un famoso esempio di equazione lineare del secondo ordine alle derivate parziali:
Qui le variabili indipendenti sono due: il tempo e una dimensione spaziale. La variabile dipendente è invece u, che dipende sia da x che da t: u=u(x,t). Se sostituiamo f(x) – che dipende unicamente dalla variabile indipendente x – con f(x,t), l’equazione rimane lineare, ma se la sostituiamo con f(u) essa diverrà non lineare appena f(u) conterrà potenze di u superiori ad 1. Va da sé che con funzioni non algebriche (esponenziali, funzioni trigonometriche) la non linearità è altrettanto evidente.
Per ulteriori dettagli consultare ad esempio: Ames, W. F. “Differential Equations”, The Engineering Handbook, CRC Press LLC, 2000
Le equazioni differenziali lineari rappresentano una classe molto importante di equazioni differenziali, sia perché possono descrivere molti sistemi in maniera esatta, sia perché spesso sono utilizzate come approssimazione di sistemi reali, grazie al fatto che sono in genere più facili da risolvere della corrispondente equazione non lineare. In questo caso si parla di problema ‘linearizzato’.
In fisica succede spesso di non saper risolvere l’equazione che descrive esattamente il problema posto. In tal caso si inizia a risolvere il problema per approssimazioni successive. Il primo passo è linearizzare le equazioni che lo descrivono. Si può infatti spesso pensare che in un intorno sufficientemente piccolo dello spazio delle soluzioni la soluzione vera non sia molto diversa da quella del sistema linearizzato.
Ciò parte dall’approssimazione di una qualsiasi funzione con la retta tangente in un punto dato. Se l’intorno considerato è abbastanza piccolo e la funzione da approssimare sufficientemente regolare, allora essa si allontanerà poco da un andamento rettilineo. Se approssimiamo la funzione f(u) con a+bu, è ragionevole pensare che la soluzione dell’equazione lineare, per valori piccoli di u, ci darà comunque delle informazioni valide anche per l’equazione non lineare. Spesso è l’unica soluzione analitica che si riesce a trovare, o comunque rappresenta un primo passo per una soluzione più generale. In molti casi, infatti, soluzioni delle equazioni differenziali non lineari vengono calcolate numericamente.
Partiamo dall’equazione dell’oscillatore armonico (intendendo con ‘ la derivazione rispetto al tempo):
Questa equazione del moto rappresenta un punto di massa m soggetto ad una forza di richiamo proporzionale alla distanza dall’origine del sistema di riferimento. Si potrebbe schematizzare come una molla ideale di massa e attrito nulli, costante elastica k che fa oscillare un piccolo peso attorno alla posizione di equilibrio.
E’ evidente da quanto detto che questa equazione è una equazione differenziale ordinaria lineare del primo ordine, la cui soluzione è x(t)=sen(wt+f), cioè il moto armonico semplice: la massa oscilla con moto armonico, e sia la posizione che la velocità che l’accelerazione sono descritti da andamenti sinusoidali nel tempo. Si trova inoltre che w2=k/m.
Complichiamo ora leggermente lo scenario: inseriamo un termine di smorzamento viscoso. Se il moto è laminare, i termini di smorzamento viscoso sono esprimibili mediante proporzionalità diretta con la velocità (termine quindi lineare nella derivata prima dell’incognita). L’equazione diventa quindi:
Anche questa equazione è lineare, ed è facile trovare delle soluzioni (avete esempi…?). Questa equazione rappresenta il moto armonico smorzato (a causa dell’attrito viscoso). A seconda dei valori relativi dei parametri si può avere smorzamento critico, sovracritico o sottocritico. Se il termine viscoso risulta dominante rispetto alle forze inerziali e di richiamo non si avranno oscillazioni, ma il semplice rilassamento verso l’equilibrio. Se le forze viscose sono trascurabili, viceversa, il moto risulterà simile a quello dell’oscillatore armonico ma con una diminuzione dell’ampiezza di oscillazione ad ogni periodo, a causa della dissipazione di energia per le forze viscose. Per tutti i dettagli della soluzione dell’equazione dell’oscillatore armonico si può consultare la pagina di wikipedia:
http://it.wikipedia.org/wiki/Oscillatore_armonico
Se però il moto non si può considerare laminare, si formano dei vortici attorno alla massa in oscillazione, ed il moto diventa turbolento. In questo caso la schematizzazione delle forze viscose come proporzionali alla velocità non è più valida, e lo schema si complica. In alcune condizioni si può ritenere valido un andamento quadratico della forza viscosa con la velocità: in tal caso l’equazione resta simile, ma il termine al quadrato fa cadere la linearità dell’equazione:
La soluzione in questo caso non è banale. Qualche considerazione generale sulle soluzioni di equazioni non lineari?
Passiamo ora al pendolo semplice. Dalla pagina di wikipedia (http://it.wikipedia.org/wiki/Pendolo_semplice) possiamo partire dall’equazione differenziale scritta in coordinate polari, ove ß è l’angolo rispetto alla verticale, r è la lunghezza del filo e g l’accelerazione di gravità:
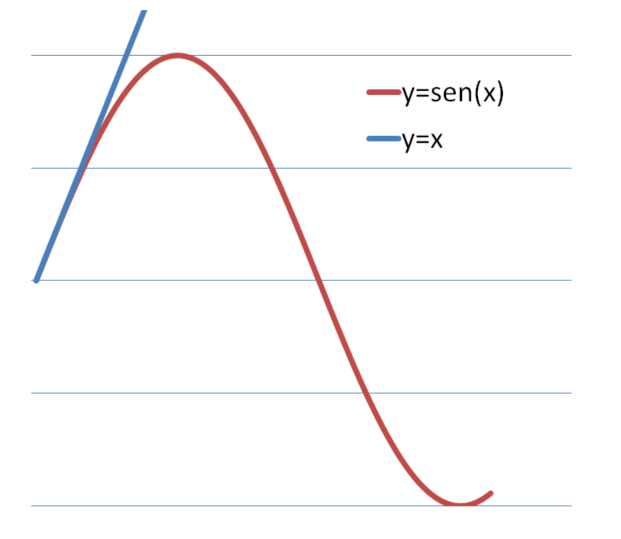
Questa equazione, che sembra molto simile a quella dell’oscillatore armonico, è però molto più insidiosa: la presenza di t (ovvero la soluzione) sotto funzione seno rende l’equazione non lineare. Per piccoli angoli il seno si può approssimare con una retta, per cui sen(x)≈x e l’equazione risulta linearizzata. Quindi il pendolo per piccoli angoli si comporta come un oscillatore armonico (figura sotto). E’ comunque anche questa un’equazione risolubile e la soluzione è riportata in tutti i testi base di meccanica.
E’ da osservare che molti tipi di oscillazioni sono descritte come oscillatori armonici, ma spesso non lo sono che in prima approssimazione. La curva di Morse, che descrive l’energia di vibrazione di una molecola biatomica, è approssimabile con il potenziale armonico, ma solo per piccole oscillazioni (http://it.wikipedia.org/wiki/Potenziale_di_Morse).
.png)
Equazioni di Navier-Stokes
Un altro caso di equazioni differenziali non lineari del secondo ordine alle derivate parziali è rappresentato dalle equazioni di Navier-Stokes, che descrivono il comportamento di un fluido in condizioni molto generali. Sebbene queste siano in grado di descrivere il moto di un fluido anche in regime turbolento, non si sa ancora trovata se esista una soluzione analitica generale, il che rappresenta uno dei problemi irrisolti della matematica. Varie soluzioni approssimate sono state trovate, ad esempio per le masse d’aria atmosferiche, sia per via analitica (sotto particolari condizioni), sia per via numerica. Per qualche approfondimento sulle equazioni di N-S si possono leggere queste due risposte precedenti:
Per concludere, accenno solamente al fatto che, una volta trovata la soluzione generale di un’equazione differenziale, essa dipende da alcuni parametri che risultano liberi e – detto molto rozzamente – possono essere determinati conoscendo le condizioni del sistema ad un istante dato (le condizioni iniziali) o come si comporta la soluzione in una data zona (condizioni al contorno). Si pensi ad esempio all’oscillatore armonico. Per determinarne precisamente il moto, occorre imporre posizione e velocità ad un certo istante, e la soluzione del’equazione del moto risulterà determinata per sempre. Piccole variazioni della posizione e della velocità comporteranno piccole variazioni della soluzione. Ciò però non è sempre vero: una proprietà molto importante di alcune equazioni differenziali è infatti la dipendenza continua dalle condizioni iniziali. Esistono equazioni in cui per quanto piccola si scelga la differenza tra due condizioni iniziali, la differenza tra le soluzioni dopo un certo tempo diventerà grande a piacere. Questa è la proprietà dei sistemi caotici, per i quali non ha molto senso parlare di soluzioni esatte, ma si riescono a caratterizzare comunque studiandone le proprietà statistiche. Un tipico esempio sono le soluzioni turbolente delle equazioni di Navier-Stokes.
Spero che da quanto detto si capisca quindi che le equazioni non lineari rappresentano una classe importante e molto vasta di fenomeni naturali (in chimica, biologia, fisica, economia) e che anzi i fenomeni descrivibili con equazioni differenziali lineari rappresentano molto spesso una approssimazione dei fenomeni reali, semplificati in modo da renderli ( si spera) risolubili da un punto di vista matematico.