Il motivo è legato proprio alla presenza di infinite dimensioni e quindi al fatto che alcune operazioni, che normalmente possiamo invertire di ordine senza che cambi il risultato, non possono più essere commutate arbitrariamente se sono coinvolte operazioni di limite. Vediamo di capire bene cosa accade.
Un operatore A, definito su un certo spazio vettoriale, è lineare se viene rispettata la seguente proprietà
![]()
qualunque sia la coppia di scalari α e β e qualunque sia la coppia di vettori u e v. Fissata una base, questa proprietà deve valere per ogni componente
![]()
dove I è l’insieme dei valori su cui varia l’indice che distingue le componenti dei vettori. I può essere un sottoinsieme finito dell’insieme dei numeri naturali (in tal caso lo spazio ha dimensione finita), può coincidere con l’insieme N dei numeri naturali (in tal caso lo spazio ha dimensione infinita numerabile) oppure può coincidere con l’insieme R dei numeri reali (in tal caso lo spazio ha dimensione infinita continua). Sono possibili altri casi ma concentreremo l’attenzione su questi.
La definizione di continuità di un operatore è un po’ più complessa. Affinché un operatore sia continuo è necessario che, preso un qualunque vettore v dello spazio e presa una qualunque successione un di elementi dello spazio che abbia v come limite, la successione che si ottiene applicando l’operatore A ad ogni singolo termine della successione un ha come limite il vettore che si ottiene applicando A direttamente a v. In simboli
A questo punto ricordiamo che, in generale, uno spazio vettoriale è ad infinite dimensioni se sono necessari infiniti vettori di base per poter scrivere tutte le combinazioni lineari che generano gli elementi dello spazio, ma ciascun elemento dello spazio è espresso da una combinazione lineare di un numero finito di elementi di una base. Un esempio di questo tipo di spazio vettoriale è P[-1,1], cioè l’insieme dei polinomi definiti sull’intervallo [_1,1]. Possiamo convincerci che è uno spazio a infinite dimensioni considerando il fatto che l’insieme di tutte le funzioni potenza intera {1, x, x2, x3, …, xn, …}, che contiene un’infinità numerabile di elementi, è una base dello spazio. Infatti se togliamo anche uno solo dei suoi elementi quelli restanti non ci permetteranno di scrivere alcuni polinomi, ma ogni polinomio, avendo un grado definito, è esprimibile combinando tra loro un numero finito di queste funzioni potenza. Consideriamo su questo spazio la norma del massimo, cioè
![]()
Consideriamo l’operatore derivata su questo spazio, che è un operatore lineare. Consideriamo inoltre la successione dei polinomi
![]()
Dato l’insieme di variazione di x, questa successione tende al polinomio identicamente nullo in tutto [_1,1], la cui immagine, mediante l’operatore derivata, è ancora il polinomio identicamente nullo. Se consideriamo invece la successione di polinomi che otteniamo derivando pn termine a termine otteniamo
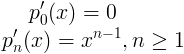
questa successione tende ad una funzione che non è un polinomio e quindi non è il polinomio identicamente nullo. Infatti il limite di xn-1, per n infinito, è zero solo per i valori di x interni a [_1,1], per x=1 il limite è 1 e per x=_1 il limite non esiste.
Questo lo si può vedere anche mediante la norma che abbiamo definito sopra. La norma di pn è 1/n, che tende a 0 per n infinito, valore che è la norma del polinomio identicamente nullo. Invece p‘n ha norma pari a 1 (tranne per n=0, ma questo non conta nel limite) e quindi anche il suo limite avrebbe norma 1, se appartenesse allo spazio in questione.
Analogamente si può considerare l’insieme delle funzioni, con dominio [0,2π] esprimibili come somma finita di funzioni seno e coseno con periodo sottomultiplo di [0,2π]. In tale spazio si considera la successione
![]()
e l’operatore derivata. Tale successione tende alla funzione identicamente nulla, mentre la successione delle derivate è cosnx, che invece non ha limite definito. Ancora una volta se si analizza il tutto con la norma del massimo si vede che sn ha norma 1/n, che tende a zero, mentre cosnx ha norma 1.
Un’ulteriore analisi può essere fatta se si considerano spazi di Hilbert, cioè spazi vettoriali in cui sono ammesse anche le combinazioni di infiniti elementi di base. Negli esempi precedenti avremmo lo spazio delle funzioni limitate in [_1,1] e infinitamente derivabili in ]_1,1[ nel caso dellba base di potenze o limitate in [0,2π] e derivabili in ]0,2π[ nel caso della base goniometrica.
Per analizzare meglio questa definizione, passiamo alle componenti e consideriamo, come chiesto dalla domanda, che A sia lineare. Fissata una certa base ciascun vettore è rappresentato da una sequenza ordinata di numeri, le sue componenti, la lunghezza di questa sequenza è pari alla dimensione dello spazio V e ogni componente è individuata da un diverso valore di un indice che appartiene a I. Allo stesso modo ogni operatore lineare è rappresentato da una sequenza, di lunghezza pari al quadrato della dimensione dello spazio, i cui elementi vengono individuati da una coppia di indici, ciascuno dei quali appartiene a I
![]()

Con questa notazione è possibile esprimere esplicitamente una componente del vettore che si ottiene da v mediante l’azione dell’operatore A
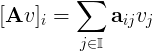
A questo punto siamo in grado di esprimere la definizione di continuità mediante le componenti e quindi analizzarla in termini di proprietà dei numeri reali e delle successioni di numeri reali. Una qualunque successione di vettori ha come limite v se le successioni di ogni singola componente hanno come limite la corrispondente componente di v
![]()
di conseguenza verrà rispettata la condizione di continuità se vale l’uguaglianza
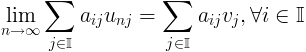
Questo è vero solo se è possibile invertire l’operazione di limite con quella di somma, perché in tal caso il limite della somma a sinistra diventa una somma di limiti eseguiti termine a termine e quindi ogni componente di un tende alla corrispondente componente di v.
Se la somma in questione è composta da un numero finito di addendi in cui l’unico termine ad essere influenzato da n è la componente unj, allora l’inversione tra imite e somma può essere svolto senza problemi. Ma ciò accade solo se lo spazio ha dimensione finita. Per tale motivo gli operatori lineari su spazi di dimensione finita sono sempre continui.
Negli spazi di dimensione infinita che non sono di Hilbert è la somma è costituita da un numero finito di addendi, ma la sua lunghezza dipende da n e quindi anche quali sono gli elementi aij ad essere coinvolti dipende da n, per cui il limite non può essere portanto all’interno ad agire solo su unj perché anche gli altri termini dipendono dalla variabile su cui interviene il limite.
In uno spazio di Hilbert la somma ha infiniti addendi, per cui la lunghezza della somma e il l’identità degli aij coinvolti non dipende da n, ma ora la somma è in realtà una serie, o addirittura un integrale (nel caso in cui l’indice di componente non è una variabile discreta ma continua). Per le serie non è automatico che invertire l’operazione di limite con quella di serie porti allo stesso risultato. Esistono tutta una serie di risultati di analisi dedicati proprio al problema di discriminare i casi in cui la commutazione è possibile da quelli in cui non lo è.
Quindi, anche se per motivi diversi caso per caso, la dimensione infinita in maniera essenziale impedisce ad un operatore di essere continuo solo sulla base della propria linearità.