L’orbita terrestre, come quella di tutti i pianeti, segue con buona approssimazione la forma geometrica di un’ellisse, come per primo riconosciuto da Keplero nel 1608. Questa osservazione empirica trova perfetta giustificazione nell’ambito della teoria della gravitazione proposta da Newton, che in generale predice che le orbite dei corpi celesti siano coniche (ellissi, parabole, o iperboli), e nel caso particolare di traiettorie legate, siano proprio ellissi, con il Sole posto in uno dei fuochi. L’orbita terrestre, essendo solo leggermente schiacciata, risulta in realtà molto simile ad una circonferenza: la lunghezza degli assi maggiore e minore differisce solo di circa una parte su 10000. Il semiasse maggiore è lungo circa 149,598 milioni di chilometri (più o meno il valore di una unità astronomica). Per caratterizzare quanto l’ellisse risulta schiacciata, si utilizza un parametro e detto eccentricità, definito nel modo seguente:
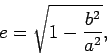 |
(1) |
dove a e b sono le lunghezze dei semiassi maggiore e minore, rispettivamente. Per l’orbita terrestre, e = 0,0167. Per calcolare la lunghezza della traiettoria percorsa dalla Terra nel corso delle stagioni, dobbiamo dunque conoscere la lunghezza di un tratto d’ellisse.
Questa derivazione, purtroppo, non è banale, nel senso che non esiste una formula semplice basata su funzioni elementari (polinomi, potenze, funzioni trigonometriche, logaritmi). Bisogna ricorrere ad una funzione integrale. Vediamo come si imposta il conto. La figura qui sotto illustra la geometria del problema. Si noti che, per rendere più chiaro l’esempio, questa ellisse è stata disegnata molto più schiacciata di come sia effettivamente l’orbita terrestre. I punti F1 ed F2 rappresentano i fuochi (uno dei quali coincide con il Sole), mentre O è il centro.
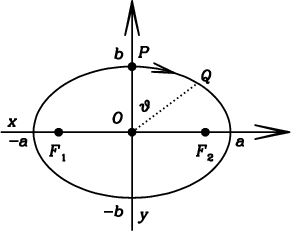
In coordinate cartesiane, l’equazione dell’ellisse si può scrivere nel seguente modo:
| (2) |
La stessa equazione si può riscrivere usando le cosiddette coordinate ellittiche. Se ϑ è l’angolo (espresso in radianti) misurato in senso orario rispetto al semiasse minore, si ha:
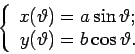 |
(3) |
Si noti che in questo modo, al variare di ϑ nell’intervallo (0, 2π), il punto (x(ϑ), y(ϑ)) percorre l’intera ellisse in senso orario a partire dal punto P = (0, b), corrispondente a ϑ = 0, come mostrato in figura. L’elemento di linea (la lunghezza di un segmento infinitesimo) è dato in coordinate cartesiane da
| (4) |
Differenziando l’equazione (3) rispetto a ϑ, si ha
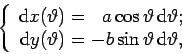 |
(5) |
da cui:
| (6) |
La lunghezza di un arco di ellisse è quindi data da
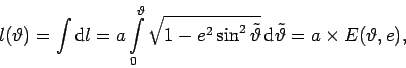 |
(7) |
dove E(ϑ,e) è una funzione speciale, chiamata integrale ellittico incompleto di seconda specie, di modulo e (il nome è tutto un programma…). Di fatto, non è possibile calcolare questo integrale in termini di funzioni più elementari (tranne che nei casi banali e = 0 oppure e = 1). L’andamento della funzione E(ϑ,e) è mostrato nella figura qui sotto per diversi valori di e. Per e = 0, l’ellisse è in realtà una circonferenza (a = b), per cui la lunghezza di un arco è data dalla ben nota relazione l = aϑ, dove a si identifica in questo caso con il raggio della circonferenza. Un altro caso particolare (degenere) si ha per e = 1 (b = 0), quando l’ellisse si riduce ad un segmento giacente sull’asse delle ordinate (percorso due volte), di lunghezza totale 4a. Si noti che in questo caso il parametro ϑ nell’equazione (3) non ha più il significato geometrico di un angolo, e la lunghezza l rappresenta la distanza percorsa da un punto che si muove lungo l’asse delle ascisse con legge del moto x(ϑ) = a sin ϑ.
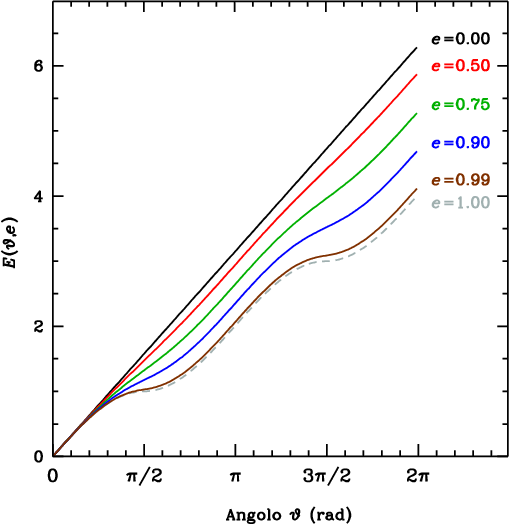
L’integrale nell’equazione (7) fornisce la lunghezza del tratto d’ellisse compreso tra i punti P (corrispondente a ϑ = 0) e Q. La lunghezza totale dell’ellisse è quindi data da L = a × E(2π,e) = 4a × E(π/2,e) = 4a × E(e), dove E(e) ≡ E(π/2,e) è il cosiddetto integrale ellittico completo di seconda specie. La figura qui sotto mostra l’andamento di L/a in funzione di e. Il caso circolare (e = 0) è quello per cui la lunghezza è massima (L = 2πa). Esistono diverse formule approssimate per calcolare il valore di L senza dover effettuare direttamente l’integrazione (si veda per esempio questo link).
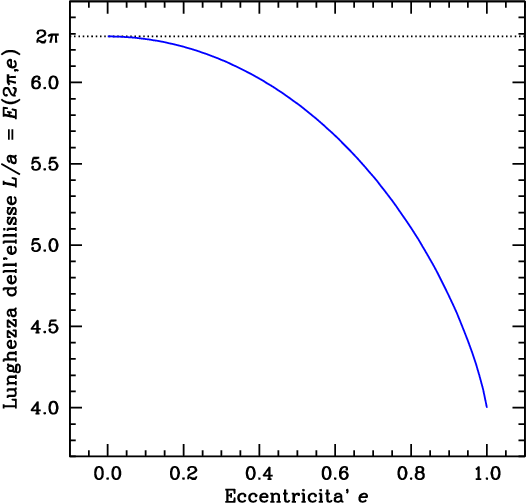
Per completare la trattazione, e per rispondere finalmente alla domanda, vediamo di calcolare la lunghezza dei tratti di orbita percorsi dalla Terra durante le quattro stagioni. Rimane da capire quali posizioni occupano i solstizi e gli equinozi nella traiettoria ellittica (in pratica, a quali valori di ϑ corrispondono). La situazione è illustrata nella figura successiva, in cui l’ellisse è stata disegnata molto poco schiacciata analogamente alla vera orbita terrestre; per questo motivo, il centro ed il fuoco sono molto vicini tra loro. Gli equinozi ed i solstizi sono indicati da rombi colorati, e la traiettoria viene percorsa in senso antiorario. Ad ogni colore corrisponde una stagione (primavera: verde; estate: rosso; arancione: autunno; blu: inverno). I segmenti tratteggiati rappresentano le linee degli equinozi e dei solstizi, che sono inclinate rispetto alla linea degli apsidi (la congiungente dell’afelio e del perielio, ossia l’asse delle ascisse nella figura). Nel 2008, l’angolo φ tra le linee degli apsidi e degi solstizi risulta di circa 12 gradi (questo angolo varia nel tempo, se pur molto lentamente, ma si tratta di un effetto trascurabile in questo contesto). Si noti che le linee degli equinozi e dei solstizi passano per il Sole, cioè per il fuoco dell’ellisse, e non per il suo centro.
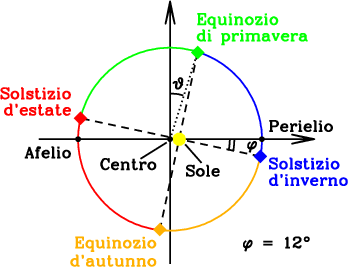
Per calcolare la lunghezza degli archi di ellisse usando la formula (7), bisogna conoscere l’angolo ϑ calcolato rispetto al semiasse minore, e quindi al centro. Il calcolo che porta a determinare i valori di ϑ corrispondenti ad equinozi e solstizi non è difficile, ma è piuttosto lungo e noioso (si tratta di fatto di un esercizio di geometria analitica). La tabella qui sotto riporta i risultati. Una volta determinati gli angoli, per calcolare la lunghezza degli archi si usa la formula (7) più volte. Per esempio, la lunghezza dell’arco corrispondente all’inverno, sarà data da a × [E(101,8°, 0,0167) – E(12,9°, 0,0167)], essendo 0,0167 l’eccentricità dell’orbita terrestre. L’ultima colonna della tabella riassume le lunghezze dei quattro archi, che è il risultato cercato.
| Stagione | Giorno di inizio | Angolo ϑ (°) | Lunghezza (milioni di km) |
| Primavera | Equinozio di primavera | 12,9 | 236,901 |
| Estate | Solstizio d’estate | 282,2 | 237,931 |
| Autunno | Equinozio d’autunno | 191,1 | 233,051 |
| Inverno | Solstizio d’inverno | 101,8 | 232,003 |
| Totale | 939,886 |
Desidero porgere i più sentiti ringraziamenti a Paolo Sirtoli e Stefano Covino per utili suggerimenti su questa risposta.
Segnalo anche i seguenti utili link tratti dal sito Mathworld (in inglese):
- http://mathworld.wolfram.com/Ellipse.html (riguardo le ellissi in generale);
- http://mathworld.wolfram.com/EllipticIntegraloftheSecondKind.html (riguardo gli integrali ellittici di seconda specie).