La domanda posta richiede una risposta più lunga, approfondita e elaborata di quanto è opportuno trattare in questo spazio, quindi in questa pagina riporto solo i fatti salienti e passaggi più delicati mettendo in evidenza gli aspetti generali dell'argomento evitando i noiosi calcoli, per i quali rimando ai siti elencati alla fine di questa breve esposizione.

Nozioni generali sulle equazioni algebriche

      Considerato un polinomio P_n(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ di grado n, è detto zero di P_n(x) un qualsiasi numero z (reale o complesso) per il quale si abbia P_n(z) = a_nzⁿ + a_n-1z^n-1 + ... + a₁z + a₀ = 0. Risulta subito evidente che, in base alla definizione appena enunciata, la ricerca degli zeri di P_n(x) è equivalente alla ricerca delle soluzioni (radici) dell'equazione algebrica:

a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ = 0.         (1)

Si può facilmente dimostrare che se z è uno zero di P_n(x) allora il polinomio x - z divide P_n(x) e viceversa, se x - z divide P_n(x), allora z è uno zero di P_n(x). Se indichiamo con P_n-1(x) il polinomio quoziente di questa divisione, può capitare che z sia anche uno zero di questo polinomio e in tal caso si dimostra che il polinomio (x - z)² divide P_n(x): in tal caso, z è detto zero di molteplicità 2. In generale, se (x - z)^k divide P_n(x), allora z è detto zero di molteplicità k e, in analogia a tale terminologia, z, è detta soluzione k-upla dell'equazione (1). Il teorema fondamentale dell'algebra afferma che P_n(x) ammette esattamente n zeri, a patto di considerare ciascuno di essi con la propria molteplicità, ossia, se z₁, z₂, ..., z_m sono zeri di molteplicità rispettivamente k₁, k₂, ..., k_m, allora k₁ + k₂ + ... + k_m = n e P_n(x) si può scrivere nel seguente modo:

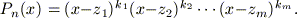
Un altro risultato importante è che se z = a + ib è una radice complessa di P_n(x), allora anche il suo complesso coniugato z' = a - ib è una radice di P_n(x); da questo segue immediatamente che se n è dispari l'equazione (1) ammette almeno una soluzione reale, mentre se n è pari essa potrebbe ammettere solo soluzioni complesse non reali.

Equazione di terzo grado

      Considerata l'equazione di terzo grado

ax³ + bx² + cx + d = 0         (2),

per quanto prima asserito si possono verificare i seguenti casi:

• 3 soluzioni reali distinte z₁, z₂, z₃;

• 3 soluzioni reali coincidenti, ossia un'unica soluzione z di molteplicità 3 (radice tripla);

• 3 soluzioni reali di cui due coincidenti, ossia una radice doppia z₁ e una radice semplice z₂;

• 1 soluzione reale z₁ e due soluzioni complesse coniugate z₂, z'₂.

Operando la sostituzione y = x + b / 3a, l'equazione (2) diviene:

y³ + 3py - 2q = 0     con 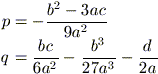,         (3)

alla quale si dà il nome di equazione depressa. Operando la sostituzione y = (z - t) essa diventa

(z - t)³ + 3p(z - t) - 2q = 0.         (4)

Tenendo presente che comunque si scelgano due numeri complessi z e t, è sempre verificata l'identità (z - t)³ + 3zt(z - t) - (z³ - t³) = 0, e confrontando quest'ultima con la (4), abbiamo che z e t devono soddisfare il seguente sistema:

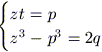        (5)

Dalla prima della (5) si ricava t = p / z e dalla seconda z³ - (p / z)³ = 2q da cui z⁶ - 2qz³ - p³ = 0, che con la sostituzione u = z³ diventa un'equazione di secondo grado nell'incognita u, u² - 2qu - p³ = 0. Risparmiandoci inutili e tediosi calcoli diciamo solamente che una volta trovate le due soluzioni u₁ e u₂ si calcolano 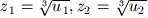e t₁ = p / z₁, t₂ = p / z₂ da cui si ricava

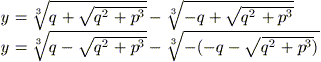
Osserviamo che queste due soluzioni coincidono (attenzione: sono la stessa soluzione, non si tratta una radice di molteplicità 2). Infatti,

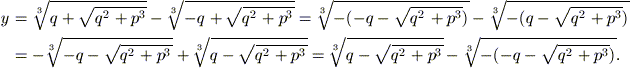
Come però detto in precedenza, un'equazione di terzo grado ammette 3 soluzioni, quindi dobbiamo cercare le altre due. Per fare ciò indichiamo con s l'unica soluzione fino a questo momento trovata, 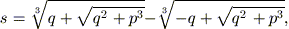; poniamo 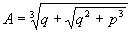e 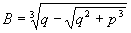e dividiamo l'equazione (3) per il polinomio (y - s), ottenendo in questo modo l'identità y² + sy + (s² + 3p) = 0, la quale è un'equazione di secondo grado. Risolvendo quest'equazione e tenendo presente che, come si può dimostrare (vi risparmio i calcoli), 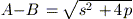si ottengono le tre soluzioni cercate dell'equazione (3):

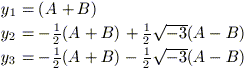
Infine, ricordando che y = x + b / 3a, si ottengono le soluzioni dell'equazione (2):

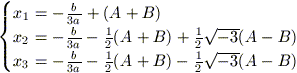    con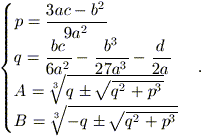     

Il fatto che nella seconda e nella terza soluzione compaia un numero immaginario (la radice quadrata di -3) non implica necessariamente che le due radici siano complesse, così come la prima radice può essere complessa anche se dalla sua espressione questo termine non appaia esplicitamente. Tutto dipende dai valori che assumono p e q, quindi A e B. Un ruolo importante lo svolge il discriminante 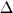 = q² + p³ e in particolare:

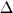•  > 0, allora A e B sono reali; tali sono anche la loro somma e la loro differenza. Ne segue che in questo caso l'equazione ha una radice reale e due radici complesse coniugate.

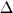•  = 0, allora A e B sono reali ed uguali; l'equazione ha tre radici reali delle quali due coincidenti (la seconda e la terza delle formule). Se poi 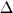 = 0 perché p = q = 0, le tre le radici sono coincidenti nel valore x = -b / 3a.

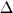•  < 0, allora le tre radici sono reali e distinte.

L'aspetto più strano in quest'ultimo caso è che, per trovare i valori reali delle tre radici, occorre trattare i numeri complessi che compaiono sotto il segno delle radici cubiche.

Equazione di quarto grado

      Passiamo adesso alla risoluzione delle equazioni di quarto grado

ax⁴ + bx³ + cx² + dx + e = 0         (8)

(ipotizziamo che sia a > 0, posizione che non lede la generalità del procedimento). Con il cambio di variabile x = y - b / 4a, si ottiene

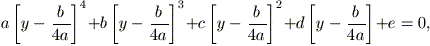
la quale, dopo vari calcoli diviene:

y⁴ + 2Ay² - By - C = 0

con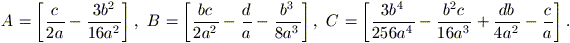

      Aggiungendo A² ad entrambi i membri si ha

y⁴ + 2Ay² + A² = A² + By + C;

tenendo presente che al primo membro si ha un quadrato perfetto, abbiamo

(y² + A)² = A² + By + C.

Aggiungendo poi w² + 2Aw + 2wy², con w da determinare in modo che al secondo membro si abbia un quadrato, otteniamo

(y² + A + w)² = 2wy² + By + (w² + 2Aw + A² + C).

Affinché al secondo membro ci sia un quadrato perfetto deve risultare che il suo discriminante (rispetto a y) sia uguale a 0, ossia 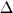 = B² - 8w(w² + 2Aw + A² + C) = 0 da cui

8w³ + 16Aw² + 8(A² + C)w - B² = 0

la quale è un'equazione di terzo grado, ed ammette almeno una soluzione reale che indichiamo con W, per cui si ha (y² + A + W)² = 2W(y + B / 4W)² e, ponendo H = (2W)^1/2, (y² + A + W)² = H²(y + B / 4W)², che fornisce due equazioni di secondo grado:

y² + Hy + (A + W - HB / 4W) = 0,
y² - Hy + (A + W + HB / 4W) = 0,

le quali, risolte, danno le soluzioni cercate.

Equazioni di grado superiore al quarto.

      L'equazione algebrica (1) si dice risolubile per radicali se le sue soluzioni sono ottenibili con un numero finito di operazioni razionali (addizioni, sottrazioni, moltiplicazioni, divisioni) ed estrazioni di radice. Le equazioni di secondo, terzo e quarto grado sono risolubili per radicali. Nel tentativo di trovare le soluzioni delle equazioni di grado superiori al quarto i matematici hanno scoperto le seguenti relazioni tra i coefficienti dell'equazione (1) e le sue radici z₁, z₂, ..., z_n:

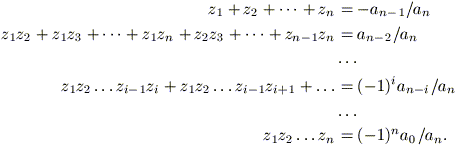
Queste relazioni, dovute a Viete, risultano fondamentali nella dimostrazione (che qui omettiamo per la sua complessità, in quanto fa uso dei concetti di strutture algebriche quali i campi, gruppi di simmetria e gruppi ciclici) del

Teorema (di Abel-Ruffini): in generale, un'equazione di grado superiore al quarto (n 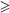 5) non è risolubile per radicali.

Questo teorema non afferma che qualunque equazione di grado n 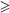 5 non è risolubile per radicali, ma che esistono equazioni non risolubili per radicali. Per esempio, x⁵ + x + 1 = 0 non è risolubile per radicali, mentre x⁵ - x⁴ - x + 1 = 0 lo è.

Bibliografia e approfondimenti