In questo articolo forniamo la descrizione formale del metodo di approssimazione ai minimi quadrati nel caso generico di polinomio di interpolazione di grado N, presentando il risultato specifico nel caso N = 2.

      Le competenze richieste per seguire la trattazione formale presentata sono di primo anno di università (facoltà scientifiche). Si veda una precedente risposta per il caso specifico N = 1 (retta interpolante), dal taglio più divulgativo, destinata a studenti di liceo.

      Sia

{(x_i, y_i), i = 1, ..., n}         [1]

l'insieme degli n punti da interpolare mediante funzione di interpolazione polinomiale di grado N:

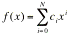.        [2]

Il metodo dei minimi quadrati consiste nel determinare gli N + 1 coefficienti C_i in modo tale che la somma degli scarti quadratici tra gli n valori y_i da interpolare e i valori della funzione interpolante f(x_i) sia minima. A tale scopo si definisce la funzione residuo nel modo seguente:

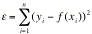        [3]

e se ne ricerca un minimo mediante il seguente sistema di N + 1 equazioni nelle N + 1 incognite c₀, ..., c_N:

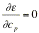,     p = 0, 1, , ..., n         [4]

esprimibile nella forma matriciale

A c = B         [5]

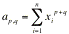,         [6]

dove x_i sono gli n valori ascissa da interpolare, mentre il vettore colonna B è espresso da

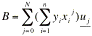,         [7]

essendo u_j il vettore colonna (0, ..., 1, ..., 0)^t costituito da soli zero ed un solo 1 nella posizione j-esima.

      Nel caso N = 2, l'espressione del sistema [4] e [5] diviene:

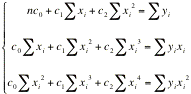        [8]

(tutte le sommatorie sono per i = 1, ..., n), un sistema di 3 equazioni nelle tre incognite c₀, c₁, c₂. Tutti gli altri termini sono infatti delle costanti date dalla sommatoria dei valori ascissa ed ordinata da interpolare.

      La matrice A della [5] è simmetrica e definita positiva, prestandosi dunque all'applicazione di algoritmi di risoluzione di sistemi matriciali piuttosto efficienti.

      Si supponga ad esempio di voler calcolare la parabola che approssimi ai minimi quadrati la serie di coppie

(x, y) = {(1, 1.2), (2, 1), (3, 1.8), (4, 2)}.

,

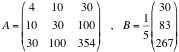da cui la soluzione c = A^-1B = (6/5, -9/50, 1/10) e la relativa parabola di interpolazione

.

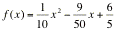Appendice

Dimostriamo ora come dalla espressione della [4] si arrivi alla formulazione matriciale [5], [6], [7].

      Calcoliamo esplicitamente la derivata della funzione residuo rispetto al generico coefficiente c_p: per brevità, utilizziamo la notazione

.

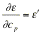Poiché la derivata della somma è pari alla somma delle derivate, espandiamo il binomio quadratico del residuo e ne calcoliamo la derivata:

.

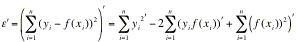Essendo y_i²una costante, la sua derivata è nulla; inoltre, applicando la regola di derivazione delle funzioni composte, si ottiene:

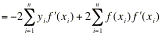 = 0.         [A1]

Calcoliamo ora la derivata prima della funzione di interpolazione f(x_i) rispetto alla variabile c_p

:

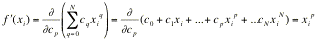trattandosi infatti di un polinomio, sopravvive solo il termine p-esimo della funzione di interpolazione, che vede la variabile di derivazione moltiplicata per la costante x_i^p.

      Sostituendo l'ultima espressione nella [A1] e semplificando si ottiene, quindi:

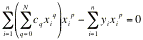
da cui, portando al secondo membro i termini noti e riarrangiando i termini della sommatoria si ottiene:

.

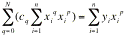Infine, applicando le proprietà del prodotto di potenze,

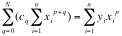
si ottiene, per p e q che variano da 0 a n, al primo e al secondo membro l'espressione del prodotto Ac e del vettore colonna B, rispettivamente.