28-06-2003
per
commenti
osservazioni
critiche
e ringraziamenti
![]()
scrivi all'autore
Una funzione matematica è invertibile solo se è
una biiezione o è invertibile anche se è soltanto iniettiva?
(risponde Gino Favero)
Data una funzione
f : A --> B, si definisce
funzione inversa della f (se esiste) una funzione
g : B --> A tale che
g(f(a)) = a per ogni a  A e
f(g(b)) = b per ogni b
A e
f(g(b)) = b per ogni b  B. Se esiste un'inversa della funzione f si
dice che f è una funzione invertibile.
B. Se esiste un'inversa della funzione f si
dice che f è una funzione invertibile.
Data la simmetria della
definizione, è immediato rendersi conto che se g è
inversa della funzione f allora è anche vero che f
è inversa della funzione g: si dice quindi che f e
g sono inverse l'una dell'altra. Per esempio, le funzioni
exp : 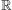 -->
--> 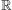 + (dove exp è la "funzione esponenziale",
exp(x) := ex) e log :
+ (dove exp è la "funzione esponenziale",
exp(x) := ex) e log : 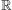 + -->
+ --> 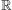 sono inverse
l'una dell'altra perché log(exp(x)) = x per
ogni x
sono inverse
l'una dell'altra perché log(exp(x)) = x per
ogni x 
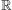 e
exp(log(x)) = x per ogni x
e
exp(log(x)) = x per ogni x 
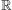 +.
+.
Ricordiamo che una funzione f : A --> B è definita come una legge che associa a ogni elemento di A un elemento di B, dove dicendo "un elemento" si intende che tale elemento deve esistere ed essere unico. Con questa definizione in mente, cerchiamo di capire quali condizioni devono essere soddisfatte da f perché possa esistere una sua funzione inversa.
Iniziamo a supporre che esista una funzione g inversa di f secondo la definizione vista sopra: allora
per ogni b
 B
l'elemento ab := g(b)
B
l'elemento ab := g(b)  A è tale che
f(ab) = f(g(b)) = b.
Ogni elemento di B è allora immagine tramite f di almeno
un elemento di A, quindi f è suriettiva.
A è tale che
f(ab) = f(g(b)) = b.
Ogni elemento di B è allora immagine tramite f di almeno
un elemento di A, quindi f è suriettiva. se a1, a2 sono due elementi di A tali che f(a1) = f(a2) deve essere a1 = g(f(a1)) = g(f(a2)) = a2, quindi f è iniettiva.
Da quanto appena visto si deduce che se f è invertibile, allora è biiettiva (cioè suriettiva e iniettiva).
D'altra parte, se
f è biiettiva, per ogni elemento b  B esiste un ab
B esiste un ab  A tale che
f(ab) = b (per la
suriettività) e tale elemento ab deve anche essere
unico (perché se a'b è un elemento di
A tale che f(a'b) = b si ha
f(ab) = f(a'b) e
quindi, per l'iniettività,
ab = a'b). Se f
è biiettiva, allora, la legge g che associa a ogni elemento
b di B l'unico elemento ab
A tale che
f(ab) = b (per la
suriettività) e tale elemento ab deve anche essere
unico (perché se a'b è un elemento di
A tale che f(a'b) = b si ha
f(ab) = f(a'b) e
quindi, per l'iniettività,
ab = a'b). Se f
è biiettiva, allora, la legge g che associa a ogni elemento
b di B l'unico elemento ab  A tale che
f(ab) = b è una funzione; si
ha inoltre evidentemente (direttamente dalla definizione di g) che
f(g(b)) = b per ogni b
A tale che
f(ab) = b è una funzione; si
ha inoltre evidentemente (direttamente dalla definizione di g) che
f(g(b)) = b per ogni b  B. Inoltre, dato un qualsiasi elemento
a
B. Inoltre, dato un qualsiasi elemento
a  A, l'elemento
a' := g(f(a))
A, l'elemento
a' := g(f(a))  A deve essere tale che
f(a') = f(a): usando ancora
l'iniettività di f possiamo allora concludere che
a' = a, cioè che
g(f(a)) = a. Abbiamo allora concluso
che se f è una funzione biiettiva esiste una funzione g
inversa di f: in altre parole, abbiamo dimostrato che una funzione
è invertibile se e solo se è biiettiva.
A deve essere tale che
f(a') = f(a): usando ancora
l'iniettività di f possiamo allora concludere che
a' = a, cioè che
g(f(a)) = a. Abbiamo allora concluso
che se f è una funzione biiettiva esiste una funzione g
inversa di f: in altre parole, abbiamo dimostrato che una funzione
è invertibile se e solo se è biiettiva.
Osserviamo che, in base
alla già notata simmetria della definizione di funzione inversa, se
g è inversa di f allora anche g è una
funzione biiettiva. È inoltre possibile rendersi conto che la
funzione inversa, se esiste, è unica: dette g e g' due
funzioni inverse della f, infatti, per ogni b  B si deve avere
f(g(b)) = b = f(g'(b))
e quindi, per l'iniettività di f,
g(b) = g'(b). È allora naturale
e corretto parlare della funzione inversa di una funzione biiettiva
f, che si indica in genere con la scrittura f-1.
B si deve avere
f(g(b)) = b = f(g'(b))
e quindi, per l'iniettività di f,
g(b) = g'(b). È allora naturale
e corretto parlare della funzione inversa di una funzione biiettiva
f, che si indica in genere con la scrittura f-1.
La risposta alla domanda del lettore sembrerebbe quindi negativa: solo le funzioni biiettive sono invertibili. È però possibile "rilassare" le proprietà che si richiedono a una funzione inversa per cercare di rendere "invertibili" (in qualche nuovo senso generalizzato) altre funzioni oltre a quelle biiettive.
Osserviamo che le due proprietà che costituiscono la biiettività (cioè l'iniettività e la suriettività) sono necessarie ciascuna per una delle due uguaglianze che costituiscono le proprietà della funzione inversa: infatti, la suriettività segue dall'uguaglianza f(g(b)) = b e l'iniettività segue dall'uguaglianza g(f(a)) = a. Una possibile generalizzazione del concetto di invertibilità si può allora dare in questo modo:
si dice che la funzione f : A --> B è invertibile a sinistra, o che ammette inversa sinistra, se esiste una funzione g : B --> A tale che g(f(a)) = a per ogni a
 A; tale g è detta inversa
sinistra della funzione f;
A; tale g è detta inversa
sinistra della funzione f; si dice che la funzione f : A --> B è invertibile a destra, o che ammette inversa destra, se esiste una funzione g : B --> A tale che f(g(b)) = b per ogni b
 B; tale g è detta inversa
destra della funzione f.
B; tale g è detta inversa
destra della funzione f.
Va da sè che se g è inversa sinistra della funzione f allora f è inversa destra della funzione g e, analogamente, che se g è inversa destra della funzione f allora f è inversa sinistra della funzione g. Inoltre, se f è invertibile a sinistra, allora f è iniettiva; analogamente, se f è invertibile a destra, allora f è suriettiva (per dimostrare queste due proposizioni basta ripetere fedelmente le argomentazioni usate in precedenza per dimostrare la suriettività e l'iniettività di una funzione invertibile). Vediamo se, come in precedenza, queste due proprietà sono in effetti una caratterizzazione delle funzioni invertibili "da una parte".
Supponiamo che f
sia iniettiva. Costruiamo la funzione
g : B --> A definendo i valori che
assume su ogni elemento b  B in
questo modo:
B in
questo modo:
se b appartiene all'insieme immagine di f (per la definizione si veda eventualmente qui), esiste un ab
 A tale che
f(ab) = b (per definizione di
insieme immagine); tale ab deve essere unico (per
l'iniettività di f, ragionando come già fatto sopra).
Definiamo allora g(b) := ab;
A tale che
f(ab) = b (per definizione di
insieme immagine); tale ab deve essere unico (per
l'iniettività di f, ragionando come già fatto sopra).
Definiamo allora g(b) := ab; se b non appartiene all'insieme immagine di f, scegliamo (non importa come) un elemento a
 A e definiamo
g(b) := a.
A e definiamo
g(b) := a.
 A si ha
che b := f(a) appartiene all'insieme immagine
di f e che a è l'unico elemento di A tale che
f(a) = b: allora
g(f(a)) = g(b) = a,
cioè g è inversa sinistra della f. Allora una
funzione è invertibile a sinistra se e solo se è iniettiva.
A si ha
che b := f(a) appartiene all'insieme immagine
di f e che a è l'unico elemento di A tale che
f(a) = b: allora
g(f(a)) = g(b) = a,
cioè g è inversa sinistra della f. Allora una
funzione è invertibile a sinistra se e solo se è iniettiva.
Analogamente, supponiamo
ora che f sia suriettiva. Questo significa che, per ogni elemento
b  B, l'insieme
Ab := {a
B, l'insieme
Ab := {a  A | f(a) = b}
non è vuoto. Senza entrare troppo nei dettagli, che si farebbero
piuttosto delicati (bisogna infatti usare l'assioma della scelta, una
proposizione che ha per la matematica degli insiemi infiniti lo stesso ruolo
e la stessa importanza che ha il postulato delle parallele per la geometria
descrittiva), "scegliendo" un particolare elemento rappresentativo
ab in ognuno degli insiemi Ab al variare
di b
A | f(a) = b}
non è vuoto. Senza entrare troppo nei dettagli, che si farebbero
piuttosto delicati (bisogna infatti usare l'assioma della scelta, una
proposizione che ha per la matematica degli insiemi infiniti lo stesso ruolo
e la stessa importanza che ha il postulato delle parallele per la geometria
descrittiva), "scegliendo" un particolare elemento rappresentativo
ab in ognuno degli insiemi Ab al variare
di b  B possiamo definire una
funzione g : B --> A tramite la
posizione g(b) := ab. Si noti che,
per definizione, f(a) = b per ogni
b
B possiamo definire una
funzione g : B --> A tramite la
posizione g(b) := ab. Si noti che,
per definizione, f(a) = b per ogni
b  B, a
B, a  Ab; allora, per ogni b
Ab; allora, per ogni b  B si ha
f(g(b)) = b, quindi g è
inversa destra della f. Allora una funzione è invertibile a
destra se e solo se è suriettiva.
B si ha
f(g(b)) = b, quindi g è
inversa destra della f. Allora una funzione è invertibile a
destra se e solo se è suriettiva.
Vale la pena di osservare che le inverse destra e sinistra, generalmente, non sono uniche. Si noti infatti che, data un'inversa sinistra g di una funzione f, si possono cambiare in qualsiasi modo i valori che g assume sugli elementi di B non appartenenti all'immagine di f ottenendo ancora un'inversa sinistra (gli unici casi in cui l'inversa sinistra è unica sono quello in cui f è biiettiva -- e quindi l'inversa sinistra coincide con l'inversa tout-court -- e quello in cui A è formato da un solo elemento, per cui esiste una sola funzione da B ad A). Analogamente, scegliendo in modo diverso i "rappresentanti" ab negli insiemi Ab si possono ottenere molte funzioni diverse tra loro e tutte inverse destre di una stessa funzione f (l'unico caso in cui questo non sia possibile è quello in cui tutti gli Ab sono formati da un solo elemento, cioè quando f è anche iniettiva: in questo caso, allora, l'inversa destra coincide con l'inversa in senso stretto).
Notiamo anche che l'inversa sinistra g di f ha un "parziale" ruolo anche di inversa destra: infatti, per ogni b appartenente all'immagine di f si ha f(g(b)) = b (mentre questa relazione non può valere per nessun b non appartenente all'immagine di f). Per l'inversa destra questo non è più vero: infatti, se g è una funzione inversa di f, l'uguaglianza g(f(a)) = a vale soltanto per i particolari rappresentanti ab scelti negli insiemi Ab.
È allora possibile dare una risposta (almeno in parte) incoraggiante alla domanda del lettore: una funzione è invertibile anche se è soltanto iniettiva o soltanto suriettiva, a condizione di non pretendere che l'inversa sia unica.
Si noti inoltre che
qualsiasi funzione f : A --> B
definisce una funzione suriettiva
f : A --> Im(f) (avente la stessa
legge e lo stesso dominio, ma differente codominio; si confronti ancora questa risposta) e quindi ammette un'inversa destra
definita su un opportuno sottoinsieme di B. A questo proposito, vale
la pena di guardare con attenzione l'esempio che (barando un pochettino) ho
portato all'inizio: la funzione esponenziale non è una funzione
suriettiva se viene considerata come funzione 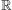 -->
--> 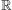 : per definire una sua
inversa destra è allora necessario "restringere" il suo codominio al
suo insieme delle immagini, che è proprio
: per definire una sua
inversa destra è allora necessario "restringere" il suo codominio al
suo insieme delle immagini, che è proprio 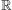 + (tale inversa destra, che è il logaritmo,
è anche inversa sinistra perché la funzione esponenziale
è iniettiva).
+ (tale inversa destra, che è il logaritmo,
è anche inversa sinistra perché la funzione esponenziale
è iniettiva).
Non è inoltre
infrequente il caso in cui un'opportuna restrizione del dominio permetta di
ottenere una funzione iniettiva a partire da una funzione che originariamente
non lo è: si pensi alla funzione
f : x --> x2, che non
è né suriettiva né iniettiva come funzione 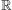 -->
--> 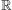 , ma che è biiettiva
come funzione
, ma che è biiettiva
come funzione 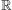 + -->
+ --> 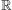 + (e la cui inversa, su tale insieme, è la
radice quadrata).
+ (e la cui inversa, su tale insieme, è la
radice quadrata).