06.04.2001

Se hai altre
curiosita'

formula qui
la tua domanda

chiede:

Ho sentito che è possibile integrare una funzione che vale zero per i razionali e uno per gli irrazionali, è vero?

Ciò mi lascia molto perplesso. Quanto farebbe l'integrale tra zero e uno di tale funzione? Se esistesse esso darebbe una misura della "densità" degli irrazionali nei numeri reali (!), avrebbe senso tutto ciò? Mi sembra impossibile che si possa affermare che tra zero e uno ci sono più irrazionali che razionali, o viceversa, è lo stesso, forse le mie perplessità nascono da un preconcetto e d'altronde non ho le conoscenze matematiche per confermare o smentire tale affermazione... Potreste chiarirmi questo curioso dubbio?

A supporto delle perplessità del nostro lettore, va detto subito che questo problema non ammette una risposta netta né immediata. In effetti, l'integrabilità della funzione citata dipende da come si decide di definire l'operatore "integrale": dobbiamo quindi spendere qualche parola per precisare questo concetto.

      L'integrale nasce dall'esigenza di calcolare l'area compresa tra una funzione e l'asse delle x in orizzontale e tra due due rette verticali arbitrarie situate alle coordinate a e b. La più famosa definizione di integrale è quella che viene insegnata anche nella scuola superiore, cioè l'integrale di Riemann: l'idea è quella riassunta nella figura 1. In pratica, dividiamo l'intervallo [a, b] in intervalli più piccoli che usiamo come base di altrettanti rettangoli; come altezze degli stessi rettangoli, prendiamo ora il valore massimo e ora il valore minimo assunti dalla funzione nei rispettivi intervalli, ottenendo così le figure costituite dai rettangoli viola e dai rettangoli gialli (la mia insegnante di liceo le chiamava "plurirettangolo esterno" e "plurirettangolo interno", ma non ho mai veramente digerito l'ampollosità del termine). Nel caso in cui le aree delle figure che otteniamo si avvicinino a un valore comune a mano a mano che si "infittisce" la partizione dell'intervallo [a, b], questo valore comune deve necessariamente essere l'area della figura di piano che ci interessa misurare.

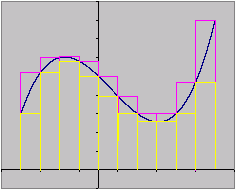
Figura 1. L'Integrale di Riemann.

Seguendo questa costruzione, è evidente che la funzione citata dal lettore non può essere integrabile sull'intervallo [0, 1]. Infatti, comunque si prendano gli "intervallini" in cui si suddivide l'intervallo [0, 1], in ogni piccolo intervallo saranno compresi almeno un punto razionale e uno irrazionale: di conseguenza, i valori estremi assunti dalla funzione su ogni intervallino saranno sempre 0 e 1 e, quindi, l'area delle due figure "approssimanti" sarà sempre, rispettivamente, 0 e 1.

Molto diversa, invece, è la definizione di integrale di Lebesgue, di cui cerchiamo di dare un'idea intuitiva senza pretesa di eccessivo rigore né di completezza; rimandiamo comunque a un testo di analisi matematica per l'università per tutti i dettagli. L'idea è quella di cercare un modo diverso per "approssimare" la funzione tramite funzioni "semplici", e tale modo è quello di operare una partizione dell'insieme delle immagini invece che del dominio.

      Supponiamo, per esempio, di voler integrare tra a e b una funzione limitata, cioè una funzione che assume valori compresi nell'intervallo [m, M]. Possiamo allora considerare una partizione di questo insieme dei valori in n intervalli [y_i-1, y_i] dove i punti y_i sono presi in modo tale che

m = y₀ < y₁ < ... < y_n = M

e ripartire il dominio in n insiemi D₁, ..., D_n tali che i valori di x compresi nell'i-esimo insieme siano esattamente quelli dell'intervallo [a, b] per cui la funzione assume valori compresi nell'intervallo [y_i-1, y_i]. Se ora è possibile conoscere in qualche senso la "misura" a_i di ognuno degli insiemi D_i, l'area della regione di piano in considerazione (che chiamiamo ancora "integrale da a a b di f(x)") soddisfa le disequazioni

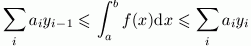
così che l'integrale esiste, come accade con l'integrale di Riemann, se "infittendo" la partizione dell'insieme delle immagini le due quantità a sinistra e a destra della disequazione qui sopra convergono allo stesso valore.

      Il vantaggio dell'integrale di Lebesgue rispetto a quello di Riemann sta nel fatto che in generale è molto più facile definire la misura di un sottoinsieme del dominio di quanto non sia "ingabbiare" una funzione "dentro" e "fuori" da delle opportune unioni di rettangoli. Sull'insieme dei numeri reali, per esempio, è definita la misura di Lebesgue, che permette di valutare l'"estensione" di un ampia famiglia di sottoinsiemi e che possiede la desiderabile proprietà che la misura di un intervallo coincide proprio con la sua lunghezza.

      Rispetto a questa definizione, si può dimostrare che la funzione citata dal lettore è integrabile. È immediato, in effetti, che l'integrale di Lebesgue della funzione considerata debba essere pari alla misura dell'insieme dei numeri irrazionali compresi tra 0 e 1 (infatti, deve essere pari alla somma tra 0 volte la misura dell'insieme dei numeri razionali e 1 volta la misura dell'insieme dei numeri irrazionali). È possibile, a questo punto, dimostrare che la misura dell'insieme dei numeri razionali appartenenti a [0, 1] è 0, perché tale è la misura di ogni sottoinsieme numerabile dell'insieme dei numeri reali: allora, la misura dell'insieme dei numeri irrazionali appartenenti a [0, 1] è pari alla misura dello stesso intervallo [0, 1], cioè 1. L'integrale di Lebesgue da 0 a 1 della funzione in oggetto è dunque 1.

Mi rendo conto che probabilmente questo risponde solo parzialmente alla domanda del lettore. In effetti, è lecito anche chiedersi come si possa affermare che i numeri irrazionali nell'intervallo [0, 1] siano in qualche senso "più" dei numeri reali. Anche qui la risposta è tutt'altro che banale e richiede una dettagliata trattazione in termini di teoria della cardinalità. È infatti possibile dimostrare che i numeri razionali sono numerabili (per la definizione di numerabilità e per qualche cenno alla teoria della cardinalità rimando a una mia precedente risposta) mentre i numeri reali hanno una cardinalità strettamente maggiore: da questo (e dal fatto che l'unione di due insiemi numerabili è numerabile) si deduce che i numeri irrazionali hanno una cardinalità strettamente maggiore di quella dei numeri razionali e, quindi, che in qualche senso è ragionevole dire che i numeri razionali sono "meno numerosi" di quelli irrazionali.