05.11.2000

Se hai altre
curiosita'

formula qui
la tua domanda

Maurizio chiede:

Devo con rincrescimento ammettere che la funzione data all’esame di maturità scientifica del corrente anno mi ha lasciato molto perplesso anche dopo aver visto la soluzione data sui giornali.

(risponde Carlo Consoli)

La funzione da studiare era la seguente:

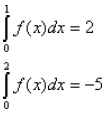
Quest'anno non ho avuto modo di seguire lo sviluppo dei compiti di maturità e, vedendo il quesito, le confesso di essere rimasto perplesso. Non si tratta di un quesito difficile ma, dato il contesto in cui è stato posto, mi fa pensare più ad uno sgambetto agli studenti, che ad una occasione di verifica e confronto delle conoscenze dei candidati.

Per quanto riguarda il quesito, la funzione cercata deve essere sicuramente continua e derivabile nell'intervallo [0,2], con derivata prima non necessariamente continua, come vedremo in seguito.

Ciò che stiamo cercando è una funzione F(x) tale che

        [1]

essendo la f(x) integrabile per ipotesi.

Dalla ipotesi, per definizione di integrale,  si ha

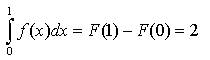                    [2]

e

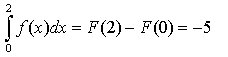                 [3]

da cui si ottiene, sottraendo la [3] dalla [2]

                     [4]

Ricordando la definizione di funzione crescente/decrescente

f(x) è crescente sse f(x₁) ³ f(x₀) per x₁ ³ x₀                                       [5]

f(x) è decrescente sse f(x₁) £ f(x₀) per x₁ ³ x₀                                  [6]

questi risultati ci indicano altri indizi sulla funzione cercata:

1.       F(x) è crescente in [0,1], perché F(1) - F(0) > 0, ovvero F(1) > F(0) ed  1 > 0 (per la [5])

2.       F(x) è decrescente in [1,2], perché F(2)-F(1) < 0, ovvero F(1) > F(2), e 2 > 1 (per la [6])

e F(x) ha un massimo locale in 1. Riscrivendo le [2] e [3], otteniamo le relazioni che definiscono la famiglia di funzioni cercate, ovvero funzioni per cui valga:

3.       F(1) = 2 + F(0)

4.      F(2)=-5 + F(0)

Proviamo a scrivere l'espressione di una funzione che soddisfi i 4 punti precedenti.

Definiamo innanzitutto la funzione

G(x)=F(x)-F(0)                   [7]

e calcoliamone la derivata prima

g(x)=G'(x)=F'(x)-F(0)'=f(x)                            [8]

perché F(0) è una costante e la derivata di una funzione costante è nulla.

La [8] suggerisce che la famiglia di funzioni cercate è definita a meno di una costante, F(0). Essendo g(x)=f(x), ovvero le funzioni derivate sono identiche, possiamo ricercare la soluzione per la funzione G(x), che consente di rimuovere la costante F(0), infatti, sostituendo le [2] e [3] nella [7], otteniamo :

G(1) = F(1)-F(0) =2          [9]

G(2) = F(2)-F(0) = -5        [10]

G(0) = F(0)-F(0) = 0         [11]

La funzione G(x) passa per i punti (0,0), (1,2) e (2, -5), la funzione più semplice che soddisfi queste condizioni è la spezzata di Fig. 1:

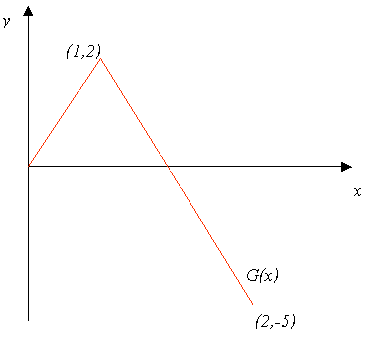
Fig. 1: Una delle funzioni nella famiglia cercata

definita dall'unione delle rette passanti per i tre punti (0,0), (1,2) e (2, -5),:

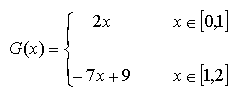             [12]

Infine, verifichiamo che la funzione trovata soddisfi le ipotesi (si osservi che questo passaggio è inutile, in quanto l'ipotesi è soddisfatta per le [8], [9] e [10]), deriviamo:

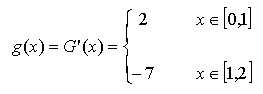       [13]

e ricalcoliamo gli integrali dell'ipotesi:

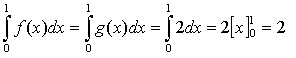
e