Vorrei avere informazioni su una curva chiamata cicloide. Qual è la sua equazione e come la si calcola.
(risponde Carlo Consoli)

Storia di "una curvità graziosissima"

Galileo cominciò ad interessarsi di una curva, più in là definita "Cicloide", sin dal 1640. Il genio pisano diceva, infatti, "Quella linea arcuata sono più di cinquant'anni che mi venne in mente il descriverla, e l’ammirai per una curvità graziosissima per adattarla agli archi d’un ponte".

Come tante altre, l’idea dello scienziato non ha tardato molto ad essere realizzata. Basta osservare i ponti dell’Arno per convincersene, magari approfittando delle vacanze Pasquali per fare una gita tra le meraviglie di Pisa.

La Cicloide è tanto bella quanto semplice da descrivere. Si immagini una bicicletta in movimento e si fissi un punto a piacere sul perimetro di una delle due ruote: la curva descritta dalla traiettoria di tale punto è detta cicloide. La circonferenza della ruota è detta circonferenza generatrice.

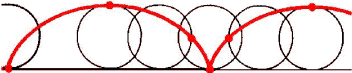
Possiamo quindi formulare la definizione della cicloide come la traiettoria generata da un punto fisso su una circonferenza generatrice che rotoli, senza slittamento, lungo un piano.

La cicloide destò l’interesse dei più grandi matematici del XVII secolo perché era la prima curva "nuova", nel senso che non era mai stata precedentemente descritta nei trattati di geometria classica. Esponenti come Pascal (celebre per i suoi studi di algebra), Roberval, Torricelli (a lui dobbiamo i primi studi sulla statica dei fluidi) e Cartesio (la geometria analitica) cominciarono ad investigarne le proprietà con interesse sempre crescente. Ai primi tre è dovuta la dimostrazione che l’area sottesa dalla cicloide tra due punti di contatto sul piano è pari al triplo dell’area della circonferenza generatrice (Galileo era inizialmente incerto su tale proprietà); Cartesio si dedicò particolarmente a sviluppare un metodo per calcolarne le tangenti. Si consideri che tali dimostrazioni erano estremamente difficoltose per l’epoca ed il cimentarsi con esse era opera da matematici di grande perizia; mancava ancora qualche anno, infatti, perché Isaac Newton (legge di Gravitazione Universale) sviluppasse il calcolo differenziale per investigare le leggi che regolano il moto dei pianeti nel cosmo. Il nostro mestiere di studenti-investigatori è sicuramente semplificato grazie all’opera di tutte queste persone.

L’equazione parametrica della cicloide

Possiamo costruire l’equazione parametrica della cicloide proprio partendo dalla definizione. Utilizziamo il Mathematica per Windows per visualizzare i passi di costruzione della curva.

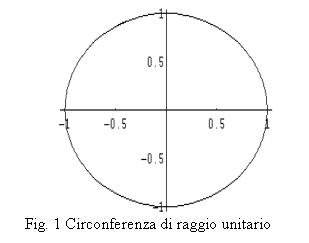
Scriviamo inizialmente l’equazione della ruota della bicicletta, ovvero una circonferenza, il cui raggio può essere impostato senza perdità di generalità ad 1.

L’equazione parametrica sul piano di una circonferenza, con senso di rotazione orario è

ruota[t_]:={Cos[-t], Sin[-t]}

e tracciamola con l’istruzione (Fig,1 )

ParametricPlot[ruota[t], {t, 0, 8*Pi}]

A questo punto, dobbiamo far avanzare la ruota lungo l’asse orizzontale in modo simulare il moto di rotolamento senza slittamento. Ciò significa che il centro di gravità della ruota (di raggio 1) avanzerà di un tratto corrispondente all’angolo di rotazione, ovvero t:

cicliode[t_]:={t+Cos[-t], Sin[-t]}

tracciamola con (Fig. 2)

ParametricPlot[cicliode[t], {t, 0, 8*Pi}]

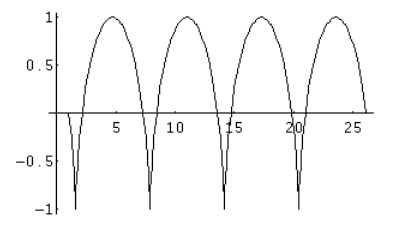Fig. 2: Cicloide sul piano con ascissa passante per il centro della circonferenza generatrice

Applichiamo ora una traslazione della cicloide di Fig. 2 per ottenerne un tracciamento "canonico", ovvero con l’ascissa passante per i punti di contatto sul piano. In particolare, trasliamo il grafico lungo l’asse delle ordinate di una distanza pari al raggio , ovvero 1, e trasliamo lungo l’asse delle ascisse diminuendo la fase del coseno di un angolo retto.

cicliode[t_]:={t+Cos[-t-Pi/2], 1+Sin[-t-Pi/2]}

tracciandola con (Fig. 3)

ParametricPlot[cicliode[t], {t, 0, 8*Pi}]

Applichiamo, infine, alcune trasformazioni sulle funzioni trigonometriche fino a ridurne l’argomento al solo parametro t. Tenendo conto delle proprietà

Sin[t+Pi/2] = Cos[t]

Cos[t+Pi/2] = -Sin[t]

Sin[-t]=-Sin[t]

otteniamo l’equazione finale della cicloide, ridotta ai minimi termini

cicliode[t_]:={t-Sin[t], 1-Cos[t]}