22-07-2003
per
commenti
osservazioni
critiche
e ringraziamenti
![]()
scrivi all'autore
In
internet ho trovato molti programmi per il calcolo approssimato delle radici
reali e complesse di un'equazione di grado n a coefficienti reali con
il metodo di Bairstow, ma non l'enunciato e la sua dimostrazione. In
conseguenza di ciò chiedo gentilmente l'algoritmo e la relativa
dimostrazione di tale metodo.
(risponde Carlo Consoli)
In rete è possibile reperire una grande quantità di materiale sull'algoritmo di Bairstow. In questa sede commentiamo il paragrafo "Real and Complex Roots of Polynomials", dagli appunti del corso di Metodi Numerici (formato Word, circa 900 kB) di un'università californiana, in cui è possibile trovare anche esempi applicativi in MatLab.
Sia f(x) = a0xn + ... + an-1x + an un polinomio di grado n. L'algoritmo numerico di ricerca delle radici di polinomi di Bairstow è basato sul seguente metodo. Dato un polinomio quadratico q(x) = x2 + ux + v (dove i coefficienti u e v sono scelti opportunamente, come diremo poi), esistono due polinomi f' e r tali che
f(x) = q(x)f'(x) + r(x).
Il polinomio f'(x) è di grado n - 2 e il resto r(x) è di grado 1, cioè una funzione lineare. Nel caso in cui r(x) = 0, si avrebbe che f(x) è un polinomio che ha due radici in comune con q(x).
Scrivendo il resto r(x) nella forma bn-1(x + u) + bn, e il polinomio f'(x) = b0xn-2 + ... + bn-3x + bn-2 si ottiene una riscrittura di f(x) nei seguenti termini:
a0xn + ... + an-1x + an = (b0xn-2 + ... + bn-3x + bn-2)(x2 + ux + v) + bn-1(x + u) + bn;
i due polinomi, per essere uguali, devono avere gli stessi coefficienti per uguali potenze di x. Questo fatto definisce la relazione di ricorrenza:
bi = ai - bi-1u - bi-2v (i = 2, 3, ..., n) [1]
ove b0 = a0 e b1 = a1 - b0u.
Il problema principale del metodo di Bairstow è scegliere i fattori u e v in modo tale che il resto r(x) sia nullo, ovvero che bn-1 e bn siano identicamente nulli. Ciò comporta la necessità di risolvere il sistema, ottenuto dalla equazione alla ricorrenze di cui sopra,
| bn-1(u, v) = 0 | [2]
| bn(u, v) = 0
| |
Le radici del sistema possono essere ottenute mediante il
metodo di Raphson-Newton per la ricerca di radici di polinomi lineari
(u e v appaiono infatti di primo grado nella equazione alle
ricorrenze). A partire da stime iniziali di u e v è
possibile determinare piccoli incrementi 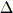 u,
u, 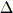 v che
risolvano il sistema [2], i.e.:
v che
risolvano il sistema [2], i.e.:
bn-1(u + 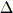 u, v + u, v + 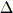 v) = 0 v) = 0 |
[3]
| bn(u + | 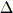 u, v + u, v + 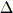 v) = 0 v) = 0
|
il metodo di Raphson-Newton prevede l'espansione della [3] in serie di Taylor bidimensionale in u e v. Per ottenere una precisione sufficiente, nella serie di Taylor ci si arresta al termine lineare:
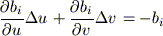 (i = n - 1, n)
[4]
(i = n - 1, n)
[4]
L'equazione alle ricorrenze [1] è ovviamente valida
anche per calcolare le derivate parziali della [4]. Ciò consente di
riscrivere la [4] applicando al posto delle derivate parziali dei
coefficienti numerici (vedi testo di riferimento per i dettagli) rispetto a
cui è possibile risolvere il sistema [4], calcolare le derivate
parziali e, quindi gli incrementi 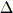 u,
u, 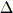 v. Si
osservi che il sistema [4] dipende dalle stime correnti dei valori u,
v.
v. Si
osservi che il sistema [4] dipende dalle stime correnti dei valori u,
v.
L'algoritmo procede quindi iterativamente nel modo seguente:
Si scelgono u, v come valori iniziali.
Si risolve il sistema [4] e si calcolano i valori corrispondenti di
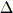 u,
u, 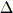 v utilizzando il valore corrente di u,
v. Se
v utilizzando il valore corrente di u,
v. Se 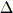 u,
u, 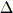 v sono prossimi allo zero, l'algoritmo termina. La
precisione delle radici trovate è strettamente correlata alla
condizione di arresto dell'algoritmo.
v sono prossimi allo zero, l'algoritmo termina. La
precisione delle radici trovate è strettamente correlata alla
condizione di arresto dell'algoritmo.
Si impostano u = u +
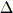 u e v = v +
u e v = v + 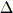 v e si re-itera dal passo 1.
v e si re-itera dal passo 1.
Al termine delle iterazioni, il sistema [3] è soddisfatto e sono determinati i valori dei coefficienti u, v per cui il resto r(x) è nullo. A questo punto le due radici del polinomio q(x) = x2 + ux + v sono in comune con il polinomio f(x). Reiterando il processo per il polinomio f'(x) si trovano a due a due tutte le radici di f(x) cercate.
Il metodo di Bairstow, essendo basato sull'algoritmo di Raphson-Newton, ne eredita le stesse caratteristiche di stabilità e robustezza. La convergenza del metodo non è sempre garantita, per assicurarne il funzionamento, occorre scegliere la coppia u, v in modo accurato.
Nel link di riferimento, è presentata la descrizione formale dell'algoritmo e vari esempi di applicazione in Matlab dei principali algoritmi numerici di ricerca degli zeri.