english version
a cura di Paolo Sirtoli
english version
![]()
 Se
pensiamo ad una generica linea immersa in un piano, la curvatura è intuitivamente
la misura di quanto essa devia rispetto alla tangente. Inoltre ci accorgiamo
immediatamente che si tratta di una proprietà locale e non globale.
In altre parole, ha senso definire la curvatura in un punto, ma non significa
nulla parlare di "curvatura di una linea".
Se
pensiamo ad una generica linea immersa in un piano, la curvatura è intuitivamente
la misura di quanto essa devia rispetto alla tangente. Inoltre ci accorgiamo
immediatamente che si tratta di una proprietà locale e non globale.
In altre parole, ha senso definire la curvatura in un punto, ma non significa
nulla parlare di "curvatura di una linea".
La curvatura in un punto P si calcola come
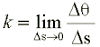 (1)
(1)
E' facile verificare che la retta, in base a questa definizione, ha curvatura nulla. Pensiamo ora alla linea curva più semplice: la circonferenza. La sua curvatura è costante per tutti i punti e vale k=1/R. Come era logico aspettarsi, quanto maggiore è il raggio, tanto minore sarà la curvatura della circonferenza; inoltre se consideriamo la retta come una circonferenza di raggio infinito, ritroviamo consistentemente che la sua curvatura è zero.
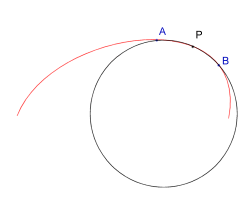 Il cerchio osculatore
Il cerchio osculatorePer misurare la curvatura k dovremmo procedere con un passaggio al limite,
che è un'operazione non sempre immediata da eseguire. Fortunatamente
esiste una formula esplicita per determinare la curvatura; a tale scopo consideriamo
due punti A e B che individuano un tratto di linea di lunghezza ![]() a cavallo del punto P. Se costruiamo la circonferenza che passa per questi tre
punti, essa approssimerà sempre meglio la linea man mano che
a cavallo del punto P. Se costruiamo la circonferenza che passa per questi tre
punti, essa approssimerà sempre meglio la linea man mano che ![]() tende a zero. Dunque se conosciamo il raggio R di questa circonferenza, possiamo
riutilizzare la formula k=1/R che avevamo visto prima!
tende a zero. Dunque se conosciamo il raggio R di questa circonferenza, possiamo
riutilizzare la formula k=1/R che avevamo visto prima!
Trovare quella circonferenza è facile perché non è altro
che il cerchio osculatore (nome dovuto a Leibniz, lo definiva circulum
osculans, vale a dire la circonferenza che "bacia" la linea in
quel punto). La formula per trovare il raggio del cerchio osculatore prevede
il calcolo della derivata prima y' e seconda y" nel punto considerato,
ed è la seguente:
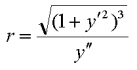 (2)
(2)
L'animazione mostra la determinazione del cerchio osculatore nel punto centrale come limite delle circonferenze che passano per i tre punti, con i due punti estremi tendenti a quello centrale.
Fonte dell'illustrazione: Yoshihiko Tazawa
E' vero che il raggio è una grandezza geometrica e dunque positiva,
ma se non ci preoccupiamo di questo aspetto, il segno di r indica semplicemente
il verso della concavità della curva rispetto al nostro sistema di assi
cartesiani.
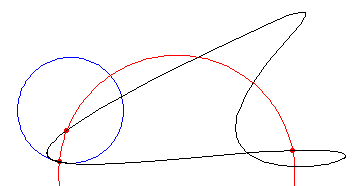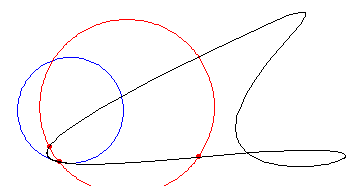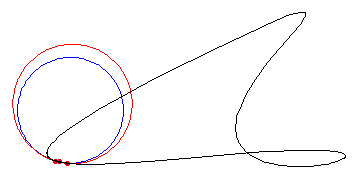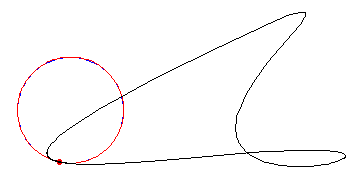
Ecco alcuni esempi significativi, che lo studente potrà agevolmente verificare
con un breve studio di funzione.
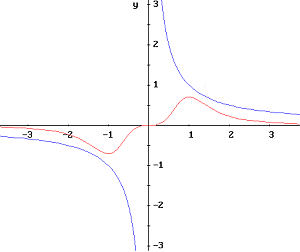
A sinistra in blu il grafico dell'equazione y=x², a destra il grafico dell'equazione
y=1/x. In rosso sono tracciati i grafici della curvatura. Si noti che il segno
della curvatura nel caso dell'iperbole equilatera rispecchia il verso della
concavità.
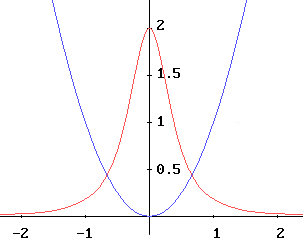
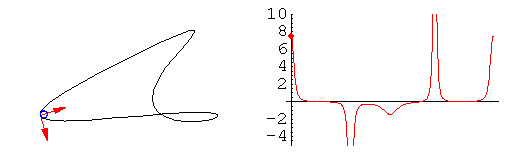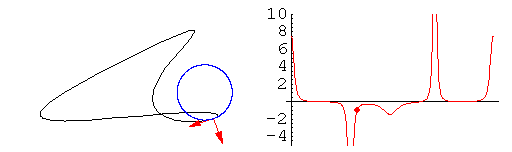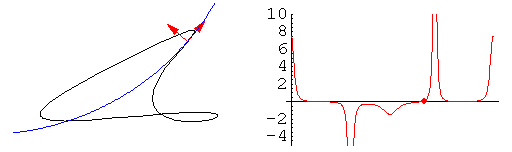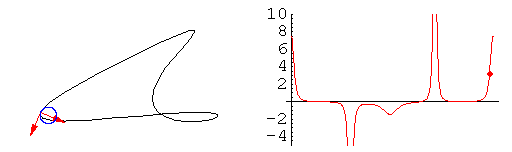
L'animazione mostra come varia la curvatura della linea, rappresentata dal cerchio osculatore in blu.
 2-D: la curvatura
di una superficie
2-D: la curvatura
di una superficieProcediamo ora con lo studio della curvatura di una superficie regolare. La
curvatura più utile in relatività e' detta anche gaussiana, in
onore del grande matematico Carl Friedrich Gauss, che ne diede la descrizione.
Consideriamo la campana schiacciata disegnata a fianco: per trovare la curvatura
di questa superficie nel punto all'apice, dobbiamo individuare la retta normale
alla superficie in quel punto. Poi andiamo a considerare tutti i piani incernierati
su tale retta: essi sezioneranno la superficie dando luogo a linee diverse,
ciascuna caratterizzata da un cerchio osculatore in quel punto, e dunque da
una curvatura. Ebbene, un teorema dovuto ad Eulero afferma che i piani che individuano
la massima curvatura e quella minima (dette curvature principali) sono perpendicolari
e Gauss definì la curvatura (gaussiana) della superficie come il prodotto
delle curvature principali. In formula:
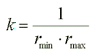 (3)
(3)
Consideriamo la sfera di raggio R: in tutti i suoi punti i piani che vanno a sezionarla descrivono sempre la stessa circonferenza, per cui la curvatura sarà in tutti i punti 1/R².
 I tre tipi di curvatura
I tre tipi di curvatura
Prestiamo ora attenzione al fatto che la curvatura ha un segno, dunque il prodotto
(3) delle due curvature principali potrà essere positivo o negativo a
seconda che i due cerchi osculatori giacciano dalla stessa parte rispetto alla
superficie, oppure da parti opposte.
Domanda: com'è la curvatura del cilindro? e quella del cono?
Contrariamente all'intuizione, queste superfici non sono affatto curve! Infatti in ogni punto possiamo individuare una sezione di curvatura minima (zero) che corrisponde ad una retta, pertanto la curvatura gaussiana, essendo il prodotto delle curvature principali, sarà nulla.
Gauss scoprì che le uniche superfici dotate di geometria intrinseca,
vale a dire che le figure quando si spostano su di esse non subiscono deformazioni,
sono soltanto tre: il piano (k=0) la sfera (k=1) e la pseudosfera(1) (k=-1). In pratica gli "abitanti" di queste superfici possono
edificare delle geometrie per descrivere il loro mondo. Invece gli abitanti
di altri mondi a curvatura non costante vedrebbero effetti stranissimi, che
non consentirebbero loro di edificare una geometria: ad esempio le figure, spostate
in certe zone, si dilaterebbero, in altre zone si contrarrebbero!
Nel 1854 Riemann ha determinato il tipo di geometria in funzione della curvatura:
è euclidea se la curvatura è nulla, sferica se la curvatura è
positiva, iperbolica se la curvatura è negativa.
Domanda: le superfici con curvatura ±2 o ±3, a differenza di quelle con curvatura ±1, non sono dotate di geometria intrinseca?
Si lo sono, la vera distinzione non sta nel valore assoluto della curvatura, ma nel segno. L'importante è che la curvatura sia la stessa in ogni punto.Domanda: il fatto di avere curvatura costante c'entra qualcosa con l'omogeneità dello spazio? e con l'isotropia?
Si. Come già detto, se la curvatura non fosse uguale per tutti i punti, le figure geometriche subirebbero deformazioni in seguito a semplici traslazioni, e dunque i punti dello spazio non sarebbero equivalenti tra loro, cioè lo spazio non sarebbe omogeneo. L'isotropia invece discende dal fatto che le curvatureprincipali sono uguali in valore assoluto. Dunque la condizione di curvatura costante non implica affatto l'isotropia: la porzione di pseudosfera visibile a lato ha in ogni punto curvatura costante e pari a -1, ma le curvature principali variano, mantenendo costante il loro prodotto. Questa pseudosfera è un esempio di spazio omogeneo ma non isotropo.
Dal punto di vista fisico, in astronomia il principio cosmologico ha come felice conseguenza il fatto che lo spazio sia omogeneo ed isotropo. Infatti ciò conduce, tra le innumerevoli possibilità, a considerare solo tre geometrie globali dell'Universo: quella piatta, quella sferica e quella iperbolica, naturalmente tutte e tre a curvatura costante.
Sulle superfici con curvatura positiva e costante viene definita una geometria
sferica. Ecco le principali proprietà:
- per un punto esterno ad una retta data non passa alcuna retta parallela ad
essa
- la somma degli angoli interni di un triangolo è maggiore di p
radianti
- il rapporto tra circonferenza e raggio è minore di 2p
- l'estensione della superficie è finita
Domanda: la Terra ha curvatura positiva, dunque sulla sua superficie è definita una geometria sferica. Dato che i paralleli della superficie terrestre non si incontrano mai, non c'è contraddizione con una delle proprietà enunciate prima?
No perché i paralleli non sono rette! Le rette sono definite nelle varietà riemanniane come le linee che rendono minima la distanza tra due punti. Nella geometria sferica le rette sono archi di cerchio massimo, vale a dire archi del cerchio che passa per i due punti considerati, e il cui centro coincide con il centro della sfera.
Vedi anche il sito "La geometria sulla sfera" di P. Lazzarini.
 La geometria iperbolica
La geometria iperbolicaSulle superfici a curvatura negativa e costante viene definita una geometria
iperbolica. Ecco le principali proprietà:
- per un punto esterno ad una retta data si possono tracciare infinite rette
parallele ad essa
- la somma degli angoli interni di un triangolo è minore di p
radianti
- il rapporto tra circonferenza e raggio è maggiore di 2p
- l'estensione della superficie è infinita
Sembrerebbe impossibile rappresentare la pseudosfera in una porzione di piano,
a causa della finitezza di quest'ultima regione. Invece esistono diverse rappresentazioni,
la più interessante è quella di Poincaré perché
è conforme, cioè conserva gli angoli e la forma delle figure geometriche.
Il celebre incisore Maurits Cornelis Escher realizzò quattro opere nelle
quali fece uso della rappresentazione di Poincaré. Qui sopra vediamo
limite del cerchio IV, meglio nota come "angeli e diavoli".
Nella geometria iperbolica tutte le figure hanno pari estensione, ma nella proiezione
sul piano euclideo esse si ammassano verso il limite del cerchio.
Per studiare le proprietà della geometria iperbolica il dipartimento
di Matematica della Rice University ha messo a punto un applet chiamato NonEuclid,
con il quale si possono verificare le proprietà enunciate sopra.
 Il maggiolone VW
Il maggiolone VWA titolo di esempio curioso mostriamo una elaborazione grafica della carrozzeria
del "mitico" maggiolone Volkswagen, i cui colori indicano la curvatura
della superficie. Si noti che dove la curvatura è negativa, i cerchi
osculatori principali giacciono da parti opposte rispetto alla superficie. Si
noti anche che il tetto, intuitivamente curvo, in realtà è solo
piegato, e la sua geometria rimane piatta.
Per completezza diciamo che i punti in cui la curvatura è positiva si
dicono ellittici, dove la curvatura è negativa iperbolici,
se la curvatura totale è nulla ma una delle curvature principali è
diversa da zero, si dicono parabolici, se invece entrambe le curvature
sono zero, planari.
 Il theorema egregium
di Gauss
Il theorema egregium
di GaussFinora abbiamo considerato linee e superfici immerse rispettivamente nel piano
e nello spazio. Dunque per valutarne la curvatura siamo ricorsi ad uno spazio
con una dimensione in più. Gauss scoprì che la curvatura è
una proprietà intrinseca, cioè può essere misurata
"da dentro", senza dover pensare a dimensioni superiori. Il grande
matematico era proverbialmente molto esigente: ad esempio scoprì la geometria
iperbolica, ma non pubblicò nulla per non dover contrastare le obiezioni
dei kantiani(2).
Stavolta però il risultato era di tale importanza che egli stesso lo
chiamò theorema egregium.
Vediamo quattro modi per misurare "internamente" la curvatura di una superficie:
1 - l'aiuola
Gli abitanti di una sfera potrebbero utilizzare una corda per tracciare una
circonferenza sul terreno (come fanno i giardinieri), misurare la lunghezza
di tale circonferenza e valutarla in rapporto a 2p volte
il raggio. Ad esempio una persona al polo nord tiene un capo di una corda lunga
10.000 km e altre persone tracciano sulla Terra con l'altra estremità
una circonferenza, che approssimativamente è l'equatore terrestre. Il
punto della questione è il seguente: gli uomini si aspettano di misurare
una circonferenza di 2p 10.000 km = 62.800 km, ma
in realtà la circonferenza misura solo 40.000 km! Da ciò si deduce
che la superficie terrestre è curva positivamente.
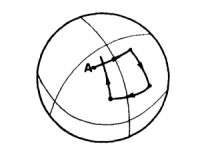 2 - il quadrato
2 - il quadrato
Un abitante di una sfera parte da un punto (A, nella figura accanto) e procede in linea retta per una quantità x. Poi svolta di 90° a destra, si sposta ancora in linea retta di x metri e poi ripete in modo da tracciare un quadrato. Se il punto di arrivo non coincide col punto di partenza, cioè se il quadrato non si chiude, allora è un chiaro indizio che quella superficie è curva.
3 - il trasporto parallelo
Un omino al polo nord ha l'incarico di marciare in direzione dell'equatore con
un vincolo strettissimo: tenere un giavellotto sempre nella stessa direzione
rispetto al suo percorso. Una volta all'equatore gli viene chiesto di spostarsi
lateralmente lungo l'equatore mantenendo fissa la direzione del giavellotto.
Infine gli viene chiesto di tornare al polo nord, con il solito vincolo. Qui,
con somma sorpresa, l'omino scopre che la direzione del giavellotto all'arrivo
non coincide affatto con quella di partenza, nonostante per tutto il cammino
egli non lo abbia mai ruotato!
 4
- le montagne di Gauss
4
- le montagne di Gauss
Tre omini sono sulla vetta di tre montagne molto lontane, ma reciprocamente
visibili, e ciascuno punta un goniometro per misurare l'ampiezza dell'arco formato
dalle altre due vette. Chiaramente ci si aspetta che la somma dei tre angoli
sia pari a p, in realtà è maggiore!
Storicamente si attribuisce a Gauss l'intenzione di misurare tale eccesso nei
calcoli relativi alla rete geodetica della regione di Gottinga, ma ciò è quasi certamente falso (si veda la biografia
di Gauss ad opera di W.K. Buhler, Springer-Verlag, 1981). Gauss infatti
era troppo accorto per non rendersi conto che gli errori sperimentali avrebbero
mascherato l'eccesso effettivo.
Analogamente a quanto si è fatto per misurare la curvatura dello spazio bidimensionale, è possibile procedere alla misura della curvatura dello spazio tridimensionale. Si tratta cioè di disegnare figure geometriche nello spazio e misurare gli scarti della loro geometria rispetto a quanto previsto dalla geometria di Euclide.
La somma degli angoli interni di un triangolo, la chiusura di un percorso quadrato, la misura del raggio di una sfera sono tutte misure utili a caratterizzare lo spazio tridimensionale. Concentriamoci sull'ultima.
Immaginiamo di tracciare una enorme sfera. Se potessimo misurarne accuratamente la superficie ed il raggio, potremmo valutare la curvatura dello spazio. Infatti ci si aspetteremmo una superficie
S=4pR². Ogni deviazione sarà da imputare alla curvatura dello spazio descritto dalla sfera.
C'è un problema: questa misura non caratterizza completamente la curvatura. Si tratta infatti di un valore medio. La specifica completa della curvatura dello spazio richiede ben sei numeri, che vanno a definire il tensore di Riemann.
 Lo spazio è curvo
Lo spazio è curvoPrendiamo il nostro pianeta, la Terra. Esso ha forma approssimativamente sferica. Se potessimo misurarne con precisione arbitraria la superficie e se potessimo anche misurarne direttamente il raggio, troveremmo una strana discrepanza. Il raggio risulta più corto di 1,5 millimetri rispetto a quello ricavato dalla formula S=4pR². Inutile rifare le misure in cerca di un errore: è proprio così.
Lo spazio racchiuso dalla Terra è curvo. Se facessimo lo stesso esperimento con il Sole, molto più grande e massiccio, otterremmo un ammanco di ben 500 metri!
Pensiamo ora ad un altro esperimento. Stavolta consideriamo una sfera che stia al di fuori della Terra, ma nelle sue vicinanze. Per meglio figurarcela, disponiamo una miriade di masse di prova a disegnare una sfera perfetta. Rimuoviamo i vincoli che tenevano le massettine al loro posto e stiamo a vedere quello che accade.
In modo quasi impercettibile, la sfera cambia forma: viene schiacciata lateralmente e viene stirata lungo la direzione del centro della Terra. Il suo volume non cambia, ma la sua forma si.
Viene spontaneo chiedersi se quindi lo spazio attorno ad un pianeta sia curvato positivamente o negativamente. La nozione di spazio a curvatura positiva, negativa o nulla, funziona solo per spazi geometrici che si chiamano "omogenei" in virtù del fatto che le proprietà metriche sono invarianti al variare del posto e ruotando attorno ad ogni posto. La presenza di una sorgente di curvatura (di gravità) rompe l'omogeneità dello spazio e non si ricade più in nella classe degli spazi tridimensionali omogenei. Quindi si ha sempre uno spazio NON euclideo, ma non è sufficiente la classificazione degli spazi omogenei per catalogarlo, ci vuole una classificazione più fine dovuta alla geometria differenziale riemanniana.
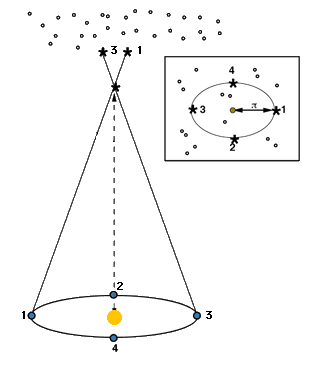 L'Universo è curvo? - 1
L'Universo è curvo? - 1 Il primo studioso a proporre un esperimento per determinare la geometria dello spazio cosmico fu il matematico Lobachevski. L'idea si basava su una caratteristica dello spazio iperbolico (l'unica geometria non-euclidea che conosceva). In un Universo di siffatta curvatura, la parallasse delle stelle non può scendere sotto un certo limite. Persino la stella più remota deve mostrare una parallasse, correlata con la lunghezza caratteristica k.
La circonferenza di un cerchio di raggio r in uno spazio iperbolico di lunghezza caratteristica k è data da
C = p k (er/k - e-r/k) = 2p k sinh(r/k)
Dato che sinh(x) = x + x3/3! +..., segue che C approssima 2p r per k che va all'infinito.
Il fatto che la parallasse di Sirio fosse di 1",24 implicava che la lunghezza caratteristica fosse almeno 166.000 unità astronomiche. Ovvero 2,6 anni-luce. Chiaramente ulteriori osservazioni di stelle più lontane, quindi con parallassi molto inferiori, forniscono valori di k molto più grandi.
Un altro tentativo di misurare direttamente la geometria dell'Universo fu effettuato negli anni trenta del secolo scorso da Edwin Hubble, contando le galassie contenute in volumi crescenti di spazio. In analogia con il caso bidimensionale, l'intenzione era quella di misurare il rapporto tra V e 4/3pR³: se fosse stato minore di 1 ciò avrebbe dimostrato che l'Universo ha curvatura positiva, in caso contrario, negativa. L'assunzione fondamentale era che le galassie fossero distribuite uniformemente, dunque il loro conteggio costituiva una misura del volume V, mentre il raggio R veniva determinato dalla misura del redshift delle galassie. Hubble arrivò alla conclusione, che egli stesso riteneva pesantemente afflitta da errori sistematici, che il volume aveva un incremento minore di quanto previsto dalla geometria euclidea, e il raggio di curvatura dell'Universo poteva essere di circa 100 milioni di anni-luce. Questo metodo è ormai abbandonato per vari motivi: principalmente perché le galassie non sono affatto distribuite uniformemente.
Il modo oggi ritenuto migliore per valutare la curvatura dell'Universo si basa sulla relatività generale: lo vedremo più avanti.
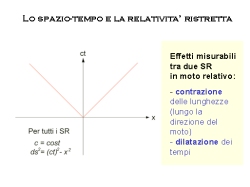 4-D*: lo spazio-tempo
di Minkowski
4-D*: lo spazio-tempo
di Minkowski Dopo la storica pubblicazione di Einstein del 1905 nella quale egli mostrò
che la simultaneità, lo spazio ed il tempo non dovevano più essere
considerati assoluti, il matematico Hermann Minkowski nel 1908 raccolse queste
indicazioni e costruì il palcoscenico matematico adeguato per la teoria
della relatività. Lo spazio ed il tempo non costituivano più entità
indipendenti, ma venivano fuse in un unica entità dotata di proprietà
stupefacenti.
A dispetto del nome, per la teoria della relatività esistono due quantità
assolute:
- per ogni sistema di riferimento la velocità della luce è costante
ed il suo valore è 299.792,458 km/s
- per ogni sistema di riferimento la separazione spazio-temporale tra due eventi
(chiamata metrica) è costante e si calcola come ds² = dx² + dy² + dz² - d(ct)² (3).
E' dunque una sciocchezza parafrasare la teoria della relatività con
l'espressione "tutto è relativo"!
Da questi due principi deriva che due osservatori in moto relativo misurano
diversamente le lunghezze e le durate, in particolare essi constatano una reciproca
contrazione delle lunghezze nella direzione del moto e una reciproca dilatazione
dei tempi.
Domanda: il segno meno nella metrica implica che lo spazio-tempo ha curvatura negativa? cioè ha una geometria iperbolica?
No, se la segnatura fosse (+ + + +) ciò implicherebbe solamente che lo spazio-tempo sarebbe una varietà riemanniana. La questione della curvatura rimane aperta: potrebbe essere positiva, nulla o negativa. Invece la segnatura (+ - - -), chiamata anche iperbolica normale, ne fa una varietà semi-riemanniana, cioè il ds² può anche essere negativo. Ciò non implica che lo spazio-tempo sia curvo negativamente e dunque iperbolico, rimane comunque piatto.
Ecco alcune proprietà dello spazio-tempo inteso come varietà semi-riemanniana:
- non esiste una lunghezza minima per una linea che unisce due eventi, esiste invece una lunghezza massima, che corrisponde al tempo proprio massimo. Il succo della legge d'inerzia nel quadro della relatività generale è che i corpi si muovono in modo da massimizzare il tempo proprio. Questo è a volte chiamato principio di massimo invecchiamento.
Domanda: se lo spazio-tempo causalmente connesso è iperbolico, c'è un qualche legame con l'incisione di Escher vista prima?
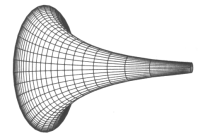
Si, questa relazione è illustrata nella figura a fianco: il cono è lo spazio-tempo di Minkowski, la cui equazione è (ct)²-x²-y²=0. Le superfici a scodella sono le due falde di un paraboloide iperbolico, che è l'analogo della sfera nella geometria iperbolica. Così come la superficie della sfera è il "mondo" per la geometria sferica, così il paraboloide iperbolico è il "mondo" per la geometria iperbolica, e si chiama spazio di Lobacevskij. Esso ha distanza unitaria dall'origine e pertanto la sua equazione è (ct)²-x²-y²=1. Ed ecco la connessione: la proiezione stereografica dal punto (-1;0;0) trasforma lo spazio di Lobacevskij nel disco di Poincarè, che giace nel piano ct=0.Fonte dell'illustrazione: "Il grande, il piccolo e la mente umana" di R. Penrose, Raffaello Cortina editore
Domanda: si è detto che il paraboloide iperbolico qui sopra ha una geometria iperbolica, però la superficie appare curvata positivamente: com'è possibile?
Non bisogna comunque confondere la curvatura di una superficie come superficie dello spazio euclideo, e il suo essere modello del piano iperbolico con una metrica non euclidea. Ad esempio, i modelli di Klein-Beltrami e i Poincaré hanno curvatura nulla se pensati come superfici euclidee (sono parti del piano euclideo), ma curvatura costante negativa se pensati come superfici iperboliche (con una misura diversa di distanza o angoli). Nel caso del paraboloide, appare sì curvato positivamente se inteso come superficie immersa nello spazio euclideo, ma la metrica di Minkowski definita su di esso fa sì che la sua geometria sia iperbolica.Domanda: non potremmo considerare il tempo come coordinata immaginaria? in tal caso t² varrebbe -|t²| e dunque la segnatura tornerebbe ad essere la "solita" (+ + + +)
Effettivamente alcuni calcoli nella teoria quantistica dei campi prevedono la continuazione analitica del tempo da coordinata reale ad immaginaria (rotazione di Wick), e lo spazio-tempo diventa riemanniano. Ad esempio la teoria di Hartle e Hawking sull'origine non singolare dell'Universo è basata sull'uso del tempo immaginario perché quando le dimensioni dell'Universo sono inferiori a 10-43m si suppone valida la gravità quantistica. Tuttavia ci sono alcune grosse difficoltà: è impossibile mettere in relazione il tempo come coordinata immaginaria con la geometria differenziale della relatività generale, inoltre la rotazione di Wick si applica solamente in assenza di gravità (cosa essa significhi in uno spazio-tempo genericamente curvo è ancora in fase di studio). A dire il vero Hawking ha dimostrato che i buchi neri hanno una temperatura equivalente, e dunque emettono radiazione, proprio usando la rotazione di Wick nell'intenso campo gravitazionale attorno ai buchi neri.
Infine, si noti che solo la metrica iperbolica normale (+ - - -) consente di distinguere(4), attraverso il segno del ds² eventi in relazione causale da eventi causalmente disgiunti.
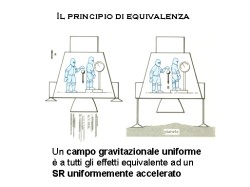 Il principio di equivalenza
Il principio di equivalenzaEsponiamo ora un altro pilastro della relatività, apparentemente scorrelato col concetto di curvatura. Due astronauti in una capsula da cui non si può vedere l'esterno svolgono alcuni esperimenti: uno lascia cadere un grave, l'altro si pesa su una bilancia.
Il punto cruciale è che non esistono esperimenti che possano distinguere tra due situazioni: la capsula in moto uniformemente accelerato e la capsula ferma in un campo gravitazionale esterno. Se non esistono prove, dobbiamo dedurre che le due situazioni sono equivalenti. Un campo gravitazionale è dunque equivalente ad un sistema di riferimento uniformemente accelerato, nel quale si manifestano forze apparenti.
A rigore questo è vero solo per un punto entro l'astronave. Tuttavia, se immaginiamo un campo gravitazionale uniforme, esso imiterà perfettamente un sistema di riferimento accelerato.
Finora abbiamo parlato dello spazio, ma la curvatura coinvolge anche il tempo, e addirittura in modo misurabile sperimentalmente. Infatti nel 1959 Pound e Rebka misero un orologio atomico alla base di una torre alta 22 metri, e uno alla sommità. Essi riuscirono a misurare che il tempo scorre più lentamente in un campo gravitazionale più intenso.
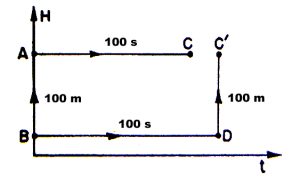 Questa è la dimostrazione che lo spazio-tempo attorno alla Terra è curvo. Vediamolo in termini geometrici. Nel grafico spazio-temporale a fianco, mettiamo un oggetto fermo alla quota h1. In 100 secondi esso traccerà la linea d'Universo BD, parallela all'asse x.
Questa è la dimostrazione che lo spazio-tempo attorno alla Terra è curvo. Vediamolo in termini geometrici. Nel grafico spazio-temporale a fianco, mettiamo un oggetto fermo alla quota h1. In 100 secondi esso traccerà la linea d'Universo BD, parallela all'asse x.
Allo stesso tempo consideriamo un altro oggetto, alla quota h2, 100 metri al di sopra di h1. Dato che si trova in un campo gravitazionale meno intenso, essendo più lontano dalla Terra, sperimenterà uno scorrere del tempo più rapido, se rapportato al tempo che scorre alla quota h1. Dunque, in 100 secondi misurati dal proprio orologio, traccerà la linea d'Universo AC, più corta di BD. I punti C e D non sono simultanei, dunque il quadrato non si chiude!
Esattamente come per il caso bidimensionale, questo significa che lo spazio-tempo è curvo.
In uno spazio-tempo piatto l'analogo della linea retta, ovvero la linea d'Universo più breve tra due eventi A e B, è un moto rettilineo uniforme.
Ricordiamo infatti che la metrica dello spazio-tempo è ds² = d(ct)² - dx² - dy² - dz².
La traiettoria rettilinea rende minima la quantità spaziale - dx² - dy² - dz². Per la parte temporale occorre ricordare che qualsiasi variazione della velocità comporta uno scorrere del tempo più lento, di un fattore rad(1-v²/c²). Quindi il termine d(ct)² è massimo per un moto uniforme. La retta nello spazio-tempo è allora la combinazione di percorso e velocità che rende massimo il termine ds², che rappresenta il tempo proprio, cioè quello percepito dall'oggetto in movimento.
Cosa succede quando lo spazio-tempo diventa curvo, ad esempio in presenza di gravità?
Il principio sopra enunciato non cambia, cioè l'oggetto si muove massimizzando il tempo proprio.
Si abbiano due punti A e B sulla superficie terrestre. Qual è la retta, o meglio la geodetica, che unisce A e B dal punto di vista dello spazio-tempo?
Ricordiamo che dobbiamo massimizzare il tempo proprio, cioè ds² = d(ct)² - dx² - dy² - dz². Se vogliamo massimizzare il tempo dovremo evitare variazioni di velocità oppure dovremo portarci lontano dalla Terra, dove il tempo scorre più velocemente. Peccato che portarci in alto implica la diminuzione di ds² perché stiamo aumentando dx², dy² e dz².
Un bel problema di ottimizzazione, dunque. Se risolviamo matematicamente il problema, troviamo che la soluzione è una parabola. Esattamente la traiettoria balistica, come se lanciassimo l'orologio con direzione e velocità iniziale ben definiti, e lasciassimo fare il resto alla gravità.
La gravità è infatti una manifestazione della curvatura dello spazio-tempo perché trasforma le linee rette di un moto in uno spazio-tempo piatto in traiettorie curve, percorse di moto accelerato, in modo che anche il tempo venga distorto.
 La geometrodinamica
La geometrodinamicaSi potrebbe chiamare in questo modo la teoria della relatività di Einstein,
dato che è la fusione di geometria (dello spazio-tempo) e dinamica, vale
a dire lo studio del moto e delle forze. La forza di gravità, visualizzata
da Newton come un vettore, è ora intesa come effetto della curvatura
dello spazio-tempo.
L'equazione fondamentale della geometrodinamica sembra semplice ed innocua,
in realtà riassume 10 equazioni non lineari e per di più le grandezze
coinvolte non sono numeri, bensì tensori. Questo capolavoro della fisica
ha consentito lo studio dei buchi neri, delle proprietà dell'Universo
e l'investigazione delle onde gravitazionali.
 La croce di Einstein
La croce di EinsteinSi tratta di una spettacolare prova della deflessione della luce da parte di
un campo gravitazionale molto intenso. La fotografia a fianco sembra mostrare
cinque oggetti distinti, in realtà sono soltanto due!
L'oggetto al centro della configurazione è una galassia massiccia che
devia i raggi luminosi provenienti da un oggetto molto più lontano e
li fa convergere verso la Terra come se provenissero da direzioni diverse.
La cosa però non può lasciarci indifferenti: i fotoni sono particelle
di massa nulla, perché mai dovrebbero rispondere ad un campo gravitazionale?
Una analogia potrà chiarire il motivo. Avete mai visto un treno in grado
di curvare? La risposta è ovviamente no, perche' il treno può
solo andare diritto! Allora in che modo esso può descrivere delle curve?
Può farlo se i binari sono curvi! La luce fa esattamente questo: procede
diritta, senza curarsi dell'attrazione gravitazionale, ma quest'ultima piega
i binari costituiti dallo spazio-tempo, e così la luce pur procedendo
diritta, si ritrova ad avere deviato. Ulteriori esperimenti hanno mostrato che
il campo gravitazionale rallenta i segnali che transitano nelle vicinanze del
Sole.
 Come si è anticipato, il metodo più
utilizzato in cosmologia per determinare la curvatura dell'Universo si basa sulla relatività generale. Secondo la teoria, la curvatura dell'Universo è completamente determinata dal suo contenuto
di materia-energia e determina il destino finale del cosmo secondo la tabella
a fianco. Il problema però è valutare con precisione il contenuto
di materia o di energia. Se ci si limita all'evidenza osservativa, contando
e "pesando" le galassie visibili, allora il contenuto dell'Universo
è circa l'1% di quanto serve per avere un Universo chiuso. Al massimo,
includendo l'elusiva materia oscura mediante valutazioni grossolane, si può
arrivare al 30%.
Come si è anticipato, il metodo più
utilizzato in cosmologia per determinare la curvatura dell'Universo si basa sulla relatività generale. Secondo la teoria, la curvatura dell'Universo è completamente determinata dal suo contenuto
di materia-energia e determina il destino finale del cosmo secondo la tabella
a fianco. Il problema però è valutare con precisione il contenuto
di materia o di energia. Se ci si limita all'evidenza osservativa, contando
e "pesando" le galassie visibili, allora il contenuto dell'Universo
è circa l'1% di quanto serve per avere un Universo chiuso. Al massimo,
includendo l'elusiva materia oscura mediante valutazioni grossolane, si può
arrivare al 30%.
Un altro metodo, che sta fornendo risultati
inattesi, è la misurazione dell'intensità luminosa e del redshift
di supernovae lontane. Ebbene, esse risultano il 25% più deboli del previsto(5),
ciò è spiegabile in due modi:
1 - l'Universo ha curvatura negativa, infatti, come per la superficie a sella
nella quale la circonferenza è più estesa di 2pR,
in tre dimensioni la luce emessa dalla stella lontana si diluisce in un guscio
più ampio di 4pR² e dunque la luminosità
risulta più bassa.
2 - l'Universo è piatto, e dunque la luminosità della supernova
è più bassa perché semplicemente si trova a maggiore distanza,
ma allora il redshift misurato è inferiore al valore richiesto dalla
distanza perché in quell'epoca l'Universo si stava espandendo più
lentamente del previsto. Se ciò è vero, possiamo dire che oggi
l'Universo si sta espandendo più velocemente del previsto, e dunque,
dato che l'unico effetto esercitato dalla materia-energia è quello di
rallentare l'espansione, allora ne deduciamo che deve esistere una misteriosa
forza repulsiva in grado di accelerare l'espansione dell'Universo. Questa forza
non è troppo misteriosa perché venne postulata dallo stesso Einstein,
sotto forma di costante cosmologica L, affinché
l'Universo fosse statico. Quando poi Hubble mise in evidenza l'espansione cosmica,
Einstein capì di avere mancato una previsione grandiosa e ritenne la
costante cosmologica l'errore più grande della sua vita scientifica.
Oggi si torna a considerare L proprio per spiegare
questa anomalia.
Lo scenario attualmente in voga prevede che l'Universo sia piatto, come richiesto
dalla teoria inflazionaria, ma che esista solo il 25% della materia per raggiungere
la densità critica, il restante 75% deriva dall'energia del vuoto espressa
dalla costante cosmologica.
Le osservazioni dei satelliti che verranno lanciati dal 2005 al 2008 consentiranno
di studiare le fluttuazioni della radiazione cosmica di fondo e, speriamo, di
sciogliere l'enigma.
 La macchina del tempo
La macchina del tempo Finora abbiamo descritto la curvatura dello spazio-tempo come principio esplicativo
della gravità. Tuttavia potrebbe anche avere un risvolto pratico attraverso
la costruzione di una macchina del tempo.
Il primo scienziato a pubblicare su una rivista scientifica seria le caratteristiche
di una macchina del tempo "realistica" è stato il fisico matematico
Frank Tipler nel 1974 (Rotating cylinders and the possibility of a global causality
violation, Physical Review D, 9, pp. 2203-2206). Nell'articolo(6) l'autore mostra che un cilindro di lunghezza infinita (ma ipotizza che anche
un cilindro di lunghezza finita potrebbe essere adeguato) la cui superficie
ruoti ad una velocità almeno pari a c/2 deforma a tal punto lo
spazio-tempo che, nelle vicinanze del cilindro, spostarsi nello spazio equivale
a viaggiare nel tempo, come se quest'ultimo fosse una dimensione puramente geometrica.
E dunque qualche giro attorno al cilindro ci porterebbe indietro nel tempo,
fino al limite massimo costituito dal momento in cui il cilindro si è
formato.
Per saperne di più:
Wheeler, Gravità e spazio-tempo, Zanichelli
Schwinger, L'eredità di Einstein, Zanichelli
Corso di laurea in Fisica
Ringrazio John Baez, Alessandro Duci, Nicola Fusco, Valter Moretti e Piergiorgio Odifreddi per le discussioni ed i chiarimenti; Mario Vitali e Pietro Rota per avermi dato l'occasione di approfondire questi argomenti.
Da aggiungere:
- il concetto di lunghezza caratteristica negli spazi curvi
- il concetto di geodetica
- lo spazio-tempo di Schwartzschild e il "tornio del vasaio"
 Per chi volesse approfondire i temi, segnalo il bel libro di Franco Nuzzi "Storia e analisi del concetto di curvatura. Dalla geometria alla cosmologia".
Per chi volesse approfondire i temi, segnalo il bel libro di Franco Nuzzi "Storia e analisi del concetto di curvatura. Dalla geometria alla cosmologia".
Può essere ordinato anche via Internet.
Note:
 (1) - Di solito si chiama pseudosfera il modello di geometria iperbolica, così come la sfera lo è per la geometria sferica. Tuttavia c'è qualche difficoltà: infatti un teorema di Hilbert dice che non esistono modelli della geometria iperbolica che siano immergibili nello spazio euclideo, e su cui si misurino distanze e angoli nella maniera euclidea.
(1) - Di solito si chiama pseudosfera il modello di geometria iperbolica, così come la sfera lo è per la geometria sferica. Tuttavia c'è qualche difficoltà: infatti un teorema di Hilbert dice che non esistono modelli della geometria iperbolica che siano immergibili nello spazio euclideo, e su cui si misurino distanze e angoli nella maniera euclidea.
Il teorema lascia solo quattro possibilità: i modelli euclidei devono o non essere immergibili nello spazio euclideo, o essere parziali, o cambiare la misura euclidea della distanza, o cambiare la misura euclidea degli angoli.
La pseudosfera vera e propria (visibile a fianco) è un modello parziale: infatti ha un buco, mentre il piano iperbolico no. Il modello di Klein-Beltrami misura gli angoli in maniera diversa da quella euclidea. Quello di Poincaré misura le distanze in maniera diversa. Il modello piu' naturale di tutti, e dal quale quelli soliti si ottengono con opportune proiezioni, e' il cosiddetto modello di Weierstrass: un iperboloide di rotazione, su cui si misuri la distanza secondo la metrica di Minkowski.
(2) - La superba costruzione della geometria euclidea, con il potente apparato deduttivo che prende le mosse dai cinque postulati e rende ragione delle proprietà di tutte le figure geometriche, aveva fatto credere a Kant e ai suoi seguaci che fosse razionalmente necessaria.
Il primo a pensare che la geometria dovesse invece ricevere conferma e determinazione dall'esperienza fu proprio Gauss.
Einstein nell'opera Il significato della relatività afferma: "sono convinto che i filosofi hanno sempre avuto un effetto dannoso sul progresso del pensiero scientifico poiché hanno sottratto molti concetti fondamentali al dominio dell'empirismo, nel quale si trovavano sotto il nostro controllo, e li hanno portati alle intangibili altezze dell'a priori".
Egli si riferiva ai concetti di spazio e di tempo, ma la citazione ci pare adeguata anche al rapporto tra geometria e realtà.
(3) - La distanza nella geometria euclidea si esprime tramite il teorema di Pitagora applicato alle coordinate. Dunque la separazione tra due punti nello spazio vale
ds² = dx² + dy² + dz².
Si definisce segnatura l'insieme dei segni delle coordinate al quadrato, in questo caso è (+ + +).
Nello spazio-tempo di Minkowski la separazione tra due eventi si esprime come
ds² = d(ct)² - dx² - dy² - dz²
la cui segnatura è (+ - - -) oppure come
ds² = dx² + dy² + dz² - d(ct)²
con segnatura (+ + + -).
Le due forme sono perfettamente equivalenti, e la scelta dell'una o dell'altra è dettata dal fatto che con la prima forma il ds² è sempre positivo all'interno del cono di luce. Alcuni libri, ad esempio quelli scritti dai fisici delle particelle, preferiscono la prima forma perché ovviamente tutta la fisica si svolge entro il cono di luce e il ds² risulta piacevolmente positivo. Invece i fisici relativisti generalmente optano per la seconda forma, più elegante perché mantiene il carattere di generalizzazione della metrica ordinaria.
Va detto che la quantità ds/c ha un preciso significato fisico: è il tempo proprio, sperimentato dal punto in moto. Sotto questa luce, vale a dire considerata come proprietà oggettiva, è perfettamente comprensibile perché ds sia uguale in tutti i sistemi di riferimento.
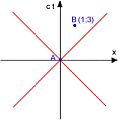
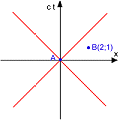
(4) - Consideriamo due coppie di eventi, la prima causalmente connessa, la seconda no. Le loro coordinate sono inventate, ma tali che nel primo caso l'evento B sia entro il cono di luce di A, mentre nel secondo caso B si trovi all'esterno.
 |
 |
||
tempo |
convenzione |
ds² = (ct)² - x² |
ds² = (ct)² - x² |
convenzione |
ds² = x² - (ct)² |
ds² = x² - (ct)² |
|
tempo |
convenzione |
ds² = (ct)² - x² |
ds² = (ct)² - x² |
convenzione |
ds² = x² - (ct)² |
ds² = x² - (ct)² |
Come si vede, qualunque sia la convenzione per la scrittura del ds², solo la metrica con il tempo reale, dunque con la segnatura (+ - - -) dà un senso alla nozione di causalità distinguendo, mediante il segno, eventi causalmente connessi da quelli non connessi.
(5) - Delle supernovae lontane possiamo misurare la luminosità apparente ed il redshift, cioè lo spostamento delle righe spettrali. Quest'ultima proprietà è fondamentale perché la legge di Hubble stabilisce una proporzione diretta tra redshift e distanza, dunque da questa misura possiamo anche risalire alla distanza della supernova.
Il punto è che se il redshift indica una distanza di 5 miliardi di anni-luce, ci si aspetta che la luminosità della supernova sia adeguata, invece è più bassa.
(6) - L'articolo di Frank Tipler digitalizzato:
pagina 1 (GIF, 210 kb)
pagina 2 (GIF, 210 kb)
pagina 3 (GIF, 210 kb)
pagina 4 (GIF, 210 kb)
Per inviare commenti, critiche, suggerimenti: paolo.sirtoli@gmail.com